Directions. The following are review problems for the MPE. We recommend you work the problems yourself, and then click "Reveal Answer" to check your answer. If you do not understand a problem, you can click the "More Examples" link below most problems to see similar questions. While there are no videos for the MPE problems, these similar examples do have videos explaining the solution.
1. Rationalize the denominator. \(\displaystyle \frac{14}{3+\sqrt{2}}\)
\[
\begin{align}
\left(\dfrac{14}{3+\sqrt{2}}\right) \left(\dfrac{3-\sqrt{2}}{3-\sqrt{2}}\right)&=\dfrac{42-14\sqrt{2}}{9-2}\\
&=\dfrac{7\left(6-2\sqrt{2}\right)}{7}\\
&=6-2\sqrt{2}
\end{align}
\]
2. Find the sum or difference as indicated, and write your answer in simplified form.\[\frac{x+2a-3}{x+a}-\frac{x+6}{2x}\]
\[\begin{align*}
\frac{x+2a-3}{x+a}-\frac{x+6}{2x} &=\left(\frac{x+2a-3}{x+a}\right) \left(\frac{2x}{2x}\right) - \left(\frac{x+6}{2x}\right)\left(\frac{x+a}{x+a}\right)\\
&=\frac{(x+2a-3)(2x)-(x+6)(x+a)}{(x+a)(2x)}\\
&=\frac{2x^2+4xa-6x-x^2-6x-xa-6a}{(x+a)(2x)}\\
&=\frac{x^2+3xa-12x-6a}{(x+a)(2x)}
\end{align*}\]
3. Factor and reduce to simplest form.\[\frac{6x^2+11xy-10y^2}{3x^2+10xy-8y^2}\]
\[ \dfrac{6x^2+11xy-10y^2}{3x^2+10xy-8y^2} = \dfrac{(3x-2y)(2x+5y)}{(3x-2y)(x+4y)}=\dfrac{2x+5y}{x+4y}\]
4. Simplify the following completely.\[\frac{\left(x^{-4}y^{2/5}\right)^{-3/4}}{x^{2/3}y^{-5/6}}\]
\[\begin{align*}
\frac{\left(x^{-4}y^{2/5}\right)^{-3/4}}{x^{2/3}y^{-5/6}}
&=\frac{x^{12/4}y^{-6/20}}{x^{2/3}y^{-5/6}}\\
&=x^{3-2/3}y^{-6/20-^-5/6}\\
&=x^{7/3}y^{32/60}\\
&=x^{7/3}y^{8/15}\\
\end{align*}\]
5. Solve the following equation: \(5(x-7)-13(x-7)-6=0.\)
\[\begin{align*}
5(x-7)-13(x-7)-6&=0\\
(x-7)(5-13)-6&=0\\
(x-7)(-8)-6&=0\\
-8x+56-6&=0\\
-8x+50&=0\\
-8x&=-50\\
x&=\dfrac{50}{8}
\end{align*}\]
6. Find the point \((x,y)\) which satisfies both equations. What is the value of \(x+y\)?\[\begin{align*} -2x+4y&=12\\ 3x-5y&=-3\end{align*}\]
Multiply \(-2x+4y=12\) by \(3\) and \(3x-5y=-3\) by 2. This gives
\[\begin{align*}
-6x+12y&=36\\
6x-10y&=-6\\
\end{align*}\]
Add these two equations and we get \(2y=30\) \(\enspace \Longrightarrow \enspace\) \(y=15\). Substituting \(y=15\) into \(3x-5y=-3\) gives \(x=24\). So the point that satisfies both equations is \((24,15)\), and the value of \(x+y\) is \(24+15 =39\).
7. Two investments are made, totaling \($10,000\). In one year, these investments yield \($650\) in simple interest. Part of the \($10,000\) is invested at \(5\frac{1}{2}\%\), and the rest at \(6\frac{3}{4}\%\). How much more money is invested at \(6\frac{3}{4}\%\)?
Let \(x\) be the amount invested at \(5\frac{1}{2}\%\) and \(y\) be the amount invested at \(6\frac{3}{4}\%\). The resulting system of equations is
\[\begin{align*}
x+y&=10,000\\
0.055x+0.0675y&=650
\end{align*}\]
Solve the system of equations to find \(x\) and \(y\).
\(x=10,000-y\) \(\enspace\Longrightarrow\enspace\) \(0.055(10,000-y)+0.0675y=650\) \(\enspace\Longrightarrow\enspace\) \(550-0.055y+0.0675y=650\) \(\enspace\Longrightarrow\enspace\) \(0.0125y = 100\) \(\enspace\Longrightarrow\enspace\) \(y=8000\). Since \(x+y=10,000\), we know that \(x=2000\), and thus \($6,000\) more is invested at \(6\frac{3}{4}\%\).
8. Given the linear equation \(2ax + 3by = 7c\), where \(a\), \(b\) and \(c > 0\), if \(x\) decreases by \(10\) units, what is the corresponding change in \(y\)?
Since \(2ax+3by=7c\) \(\enspace\Longrightarrow\enspace\) \(3by=7c-2ax\) \(\enspace\Longrightarrow\enspace\) \(y=\dfrac{7c-2ax}{3b}=\dfrac{-2a}{3b}x +\dfrac{7c}{3b}\). If \(x\) decreases by \(10\), then we know \(y=\dfrac{-2a}{3b}(x-10)+\dfrac{7c}{3b}=\dfrac{-2ax}{3b}+\dfrac{20a}{3b}+\dfrac{7c}{3b}\), so \(y\) will increase by \(\dfrac{20a}{3b}\).
9. Line \(A\) passes through the points \((2k+3, 4k−6)\) and \((−2, 16)\). Find the value of \(k\) if line \(A\) has a slope of \(0\).
\(\dfrac{4k-6-16}{2k+3+2}=0\) \(\enspace\Longrightarrow\enspace\) \(\dfrac{4k-22}{2k+5}=0\) \(\enspace\Longrightarrow\enspace\) \(4k-22=0\) \(\enspace\Longrightarrow\enspace\) \(k=\dfrac{22}{4}=5.5\)
10. Jay wants to make a box, with no lid (or top), out of a \(10'' \times 6''\) rectangular piece of cardboard. If Jay cuts squares with dimensions \(x\) by \(x\) out of each corner of the cardboard, and then folds up the corners to make an open box, find a function that represents:
- The volume of the box.
- The surface area of the box.
- \(V=(10-2x)(6-2x)x=4x^3-32x^2+60x\)
- \[\begin{align*} SA&=2x(6-2x)+2x(10-2x)+(6-2x)(10-2x)\\&=12x-4x^2+20x-4x^2+60-32x+4x^2\\&=-4x^2+60\end{align*}\]
11. Solve for \(x\) in the inequality \(\dfrac{5x+2}{x-10}\geq 3.\)
\[\begin{align*}
\dfrac{5x+2}{x-10}&\geq 3\\
\dfrac{5x+2}{x-10}-3&\geq 0\\
\dfrac{5x+2-3(x-10)}{x-10} &\geq 0\\
\dfrac{5x+2-3x+30}{x-10}&\geq 0\\
\dfrac{2x+32}{x-10}&\geq 0
\end{align*}\]
The expression \(\dfrac{2x+32}{x-10}\) will be greater than or equal to zero on \((-\infty, -16]\cup(10,\infty)\).
12. Find the domain of the function below.\[f(x)=\dfrac{\sqrt{x^2-3x-4}}{6x^2-54}\]
To find the domain of \( f(x)=\dfrac{\sqrt{x^2-3x-4}}{6x^2-54}\) we know \(x^2-3x-4\geq 0\) and \(6x^2-54 \neq 0\). \(x^2-3x-4\geq 0\) for \((-\infty, -1]\cup[4,\infty)\) and \(6x^2-54\neq 0\) for \((-\infty,-3)\cup(-3,3)\cup(3,\infty)\). So the domain of \(f(x)\) is \( (-\infty,-3)\cup (-3,-1]\cup [4,\infty).\)
13. Find the domain of the function below. \[f(x)=\left\{\begin{array}{cc}\dfrac{2x^2+13}{x^2-1}, & x<0\\ \dfrac{5x-26}{x+2}, & x\geq 0\end{array} \right.\]
For the function \(\dfrac{2x^2+13}{(x+1)(x-1)}\) on \( x<0\) the domain is \((-\infty,-1)\cup(-1,0)\). For the function \(\dfrac{5x-26}{x+2}\) on \(x\geq 0\) the domain is \([0,\infty)\). So for the function \(f(x)\), the domain is \( (-\infty,-1)\cup (-1,\infty)\).
14. Find the \(x\)-intercept(s) of the function \(f(x)=\dfrac{6x^2-7x-5}{4x^2-12x-7}\), if any exist.
\[\begin{align*}
f(x)&=\dfrac{6x^2-7x-5}{4x^2-12x-7}\\
&=\dfrac{(2x+1)(3x-5)}{(2x+1)(2x-7)}\\
&=\dfrac{3x-5}{2x-7}
\end{align*}\]
The \(x\)-intercept is where \(3x-5=0\) \(\enspace\Longrightarrow\enspace\) \(x=\dfrac{5}{3}\).
15. Find the vertical and horizontal asymptote(s) of the function \( f(x)=\dfrac{6x^2-7x-5}{4x^2-12x-7}\), if any exist.
\[\begin{align*}
f(x)&=\frac{6x^2-7x-5}{4x^2-12x-6}\\
&=\frac{(2x+1)(3x-5)}{(2x+1)(2x-7)}\\
&=\frac{3x-5}{2x-7}
\end{align*}\]
The vertical asymptote is where \(2x-7=0\) so it is \(x=\dfrac{7}{2}\).
The horizontal asymptote is at \(y= \dfrac{6}{4}\) which reduces to \(y= \dfrac{3}{2}\).
16. Find the \(x\)- and \(y\)-intercepts for the function \(f(x)=x^3-9x.\)
To find the \(x\)-intercepts solve \(f(x)=0\) \(\enspace \Longrightarrow\enspace \) \(x(x+3)(x-3)=0\) \(\enspace \Longrightarrow\enspace \) \(x=0,\pm 3\).
To find the \(y\)-intercept, substitute \(x=0\) \(\enspace \Longrightarrow\enspace \) \(0^3-9(0)=0\). Hence, the \(y\)-intercept is \(y=0\).
17. Find the domain of the following functions:
- \(f(x)=\sqrt{-x^2-4x+5}\)
- \(g(t)=\ln(4t-3)\)
- \(h(x)=\dfrac{1}{x^3+3x^2-x-3}\)
- We must have \(−x^2−4x+5\geq 0\) for \(f(x)\) to be defined. Thus, \((−x+1)(x+5)\geq 0\) which occurs on \([−5, 1]\). Thus, the domain of \(f(x)\) is \([−5, 1]\).
- We must have \(4t − 3 > 0\) for \(g(t)\) to be defined. Thus, the domain for \(g(t)\) is \(\left(\dfrac{3}{4},\infty\right)\).
- We must have \(x^3+3x^2-x-3\neq 0\) for \(h(x)\) to be defined. \[\begin{align*} x^3+3x^2-x-3&\neq 0\\ x^2(x+3)-(x+3)&\neq 0\\ (x+3)\left(x^2-1\right) &\neq 0 \\(x+3)(x-1)(x+1)&\neq 0 \end{align*}\] So \(x\neq \pm 1\) and \(x\neq -3\). Thus, the domain of \(h(x)\) is \((-\infty, -3)\cup (-3,-1) \cup (-1,1) \cup (1,\infty)\).
18. Simplify the expression \( \dfrac{2}{\sqrt{x^5}} \left(\sqrt[3]{4x}\right).\)
\[\begin{align*}
\left( \dfrac{2}{\sqrt{x^5}}\right) \left(\sqrt[3]{4x}\right) &= \left(2x^{-5/2} \right) (4x)^{1/3}\\
&=\left(2x^{-5/2}\right) \left(4^{1/3}\cdot x^{1/3}\right) \\
&=\left(2x^{-5/2}\right)\left( \left(2^2\right)^{1/3}x^{1/3}\right)\\
&=\left(2x^{-5/2}\right)\left(2^{2/3}x^{1/3}\right)\\
&=\dfrac{2^{5/3}}{x^{13/6}}
\end{align*}\]
19. If we begin with the graph of \(f(x) = x^2\) and shift \(f (x)\) 4 units to the right, shrink f (x) vertically by a factor of \(\frac{1}{2}\), and then shift \(f(x)\) upward 10 units, write the equation for the transformed graph.
The transformed graph is \(g(x)=\dfrac{1}{2}(x-4)^2+10.\)
20. Solve the following equation for \(x\).\[\log(x+2)+\log(x-1)=1\]
The domain of \(\log(x+2)\) is \((-2,\infty)\). The domain of \(\log(x-1)\) is \((1,\infty)\). So, the domain of \(\log(x+2)+\log(x-1)\) is \((1,\infty)\). Now, use properties of logarithms to solve the equation.
\[\begin{align*}
\log(x+2)+\log(x-1)&=1\\
\log\left[ (x+2)(x-1)\right] &= 1\\
(x+2)(x-1)&=10^1\\
x^2+x-2&=10\\
x^2+x-12&=0\\
(x+4)(x-3)&=0\\
x&=-4,3
\end{align*}\]
Since \(x=-4\) is not in the domain, \(x=3\) is the only solution.
21. Factor the expression below completely. \[3x^2\left(4x^2+1\right)^8+64x^4\left(4x^2+1\right)^7\]
![Accordion CMSUser Widget]()
\[\begin{align*}
3x^2\left(4x^2+1\right)^8+64x^4\left(4x^2+1\right)^7 &= x^2\left(4x^2+1\right)^7 \left(3\left(4x^2+1\right)+64x^2\right)\\
&=x^2\left(4x^2+1\right)^7\left(12x^2+3+64x^2\right)\\
&=x^2\left(4x^2+1\right)^7\left(76x^2+3\right)
\end{align*}\]
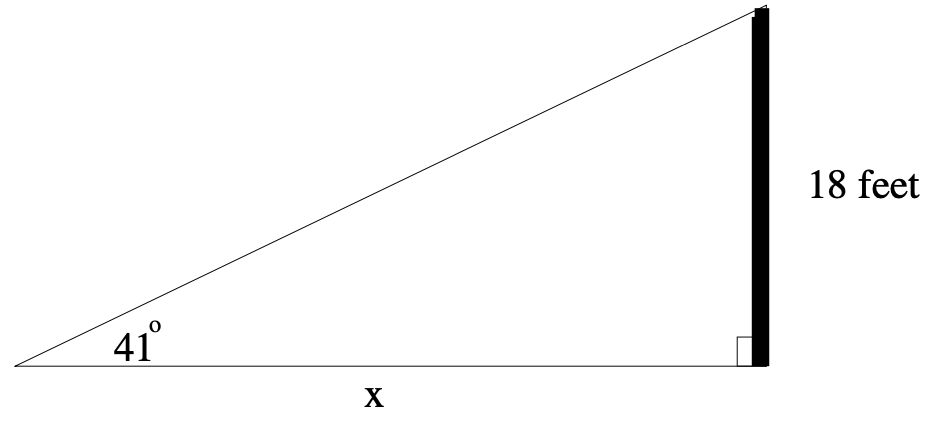
22. How far from the base of an \(18\) foot tall pole must a person be standing if the angle of elevation from the ground to the pole is \(41^\circ\)?
Refer to the figure below. We know that \(\tan (41^\circ)=\dfrac{18}{x}\). So, \(x=\dfrac{18}{\tan 41^\circ}\) or \(x=18\cot(41^\circ)\). So, the person must be \(18\cot(41^\circ)\) feet from the base of the pole.
23. Find \(f\circ g\) (also denoted \(f(g(x))\)) if \(f(x)=\dfrac{x}{x+1}\) and \(g(x)=\dfrac{2}{x}\). Simplify.
\[\begin{align*}
f\circ g &= \frac{ \frac{2}{x}}{\frac{2}{x}+1}\\
&= \frac{ \frac{2}{x}}{\frac{2}{x}+\frac{x}{x}}\\
&=\frac{ \frac{2}{x}}{\frac{2+x}{x}}\\
&=\frac{2}{x}\cdot \frac{x}{2+x} \\
&=\frac{2}{2+x}
\end{align*}\]
24. Perform the indicated operations and simplify. \[\frac{8}{x+1}-\left(\frac{y}{z+2} \div \frac{y-4}{w}\right)\]
\[\begin{align*}
\frac{8}{x+1}-\left( \frac{y}{z+2} \div \frac{y-4}{w}\right) &= \frac{8}{x+1}-\left( \frac{y}{z+2} \cdot \frac{w}{y-4}\right)\\
&=\frac{8}{x+1} - \left( \frac{yw}{(z+2)(y-4)}\right) \\
&=\frac{ 8(z+2)(y-4)-yw(x+1)}{(x+1)(z+2)(y-4)}\\
&=\frac{8zy-32z+16y-64-ywx-yw}{(x+1)(z+2)(y-4)}
\end{align*}\]
25. Solve the equation \(e^{2x}-2e^x-3=0\) for \(x.\)
First, factor the equation: \(e^{2x}-2e^x-3=(e^x)^2-2e^x-3=(e^x-3)(e^x+1)\). Solving \((e^x-3)(e^x+1)=0\) \(\enspace \Longrightarrow\enspace \) \(e^x-3=0\) or \(e^x+1=0\) \(\enspace \Longrightarrow\enspace \) \(e^x=3\) or \(e^x=-1\). But \(e^x\) will never be negative, so the only solution is \(e^x=3\) \(\enspace \Longrightarrow\enspace \) \(x=\ln(3)\).
26. Find the equation of the line passing through the point \((5,1)\) with a slope of 7. Use the equation you find to determine the value of \(y\) when \(x=-4.\)
Using the point-slope equation, we get \(y-1=7(x-5)\) \(\enspace \Longrightarrow\enspace \) \(y=7x-35+1\) \(\enspace \Longrightarrow\enspace \) \(y=7x-34\). Using this to find \(y\) when \(x=-4\) gives \(y=7(-4)-34\) \(\enspace \Longrightarrow\enspace \) \(y=-62\).
27. If \(f(x)=\sqrt{x+4}\), find and simplify \(\dfrac{f(2+h)-f(2)}{h}.\)
\[\begin{align*}
\dfrac{f(2+h)-f(2)}{h} &=\dfrac{\sqrt{2+h+4}-\sqrt{2+4}}{h}\\
&=\left(\dfrac{\sqrt{6+h}-\sqrt{6}}{h}\right) \cdot \left( \dfrac{\sqrt{6+h}+\sqrt{6}}{\sqrt{6+h}+\sqrt{6}}\right)\\
&=\dfrac{6+h-6}{h\left(\sqrt{6+h}+\sqrt{6}\right)}\\
&=\dfrac{1}{\sqrt{6+h}+\sqrt{6}}
\end{align*}\]
28. Simplify \(\dfrac{ \left(x^2y^4\right)^5\left( x^3y\right)^{-3}}{xy}.\)
\[\begin{align*}
\dfrac{ \left(x^2y^4\right)^5\left( x^3y\right)^{-3}}{xy}
&=\dfrac{x^{10}y^{20}x^{-9}y^{-3}}{xy}\\
&=\dfrac{xy^{17}}{xy}\\
&=y^{16}
\end{align*}\]
29. Simplify \(\sqrt[3]{\left(a^3b\right)}\sqrt[3]{64a^4b^2}.\)
\(\sqrt[3]{\left(a^3b\right)}\sqrt[3]{64a^4b^2}=\sqrt[3]{64a^7b^3}=4a^2b\left(\sqrt[3]{a}\right)\)
30. Perform the operations indicated and simplify.\[\frac{x^2}{x^2-x-2}-\frac{4}{x^2+x-6}+\frac{x}{x^2+4x+3}\]
\[\begin{align*}
\frac{x^2}{x^2-x-2}&-\frac{4}{x^2+x-6}+\frac{x}{x^2+4x+3}\\
&=\frac{x^2}{(x-2)(x+1)}-\frac{4}{(x+3)(x-2)}+\frac{x}{(x+1)(x+3)}\\
&=\left(\frac{x+3}{x+3}\right)\left(\frac{x^2}{(x-2)(x+1)}\right) -\left(\frac{x+1}{x+1}\right) \left(\frac{4}{(x+3)(x-2)}\right)+\left(\frac{x-2}{x-2}\right)\left(\frac{x}{(x+1)(x+3)}\right)\\
&= \frac{x^3+3x^2-4x-4+x^2-2x}{(x+3)(x-2)(x+1)}\\
&=\frac{x^3+4x^2-6x-4}{(x+3)(x-2)(x+1)}
\end{align*}\]
31. Find all zeros, horizontal, and vertical asymptotes for \(f(x)=\dfrac{3x^2-14x-5}{4x^2-17x-15}.\)
Factor and simplify: \(f(x)=\dfrac{3x^2-14x-5}{4x^2-17x-15}=\dfrac{(3x+1)(x-5)}{(4x+3)(x-5)}=\dfrac{3x+1}{4x+3}\). This yields a zero of \(x=-\dfrac{1}{3}\), a vertical asymptote of \(x=-\dfrac{3}{4}\), and a horizontal asymptote of \(y=\dfrac{3}{4}\).
32. If \(\theta\) is in Quadrant II, and \(\sin(\theta) = \dfrac{1}{7}\), what is \(\cos(\theta)?\)
Using the identity \(\cos^2 \theta + \sin^2 \theta = 1\), we find that \(\cos^2 \theta = 1-\sin^2\theta=1-\dfrac{1}{49}=\dfrac{48}{49}\). This gives us \(\cos \theta= \pm \sqrt{\dfrac{48}{49}}=\pm \dfrac{\sqrt{48}}{7} = \pm \dfrac{4\sqrt{3}}{7}\). Since \(\theta\) is in quadrant II, \(\cos \theta <0\), hence \(\cos \theta = -\dfrac{4\sqrt{3}}{7}\).
33. Use the properties of logarithms to expand the expression \( \ln \left( \dfrac{\sqrt{x}y^5}{(z+1)^4}\right).\)
We know \(\ln(ab)=\ln a + \ln b\), \( \ln \left(\dfrac{a}{b}\right)=\ln a - \ln b\), and \( \ln a^b =b \ln a\). Using these properties, we obtain
\[\begin{align*}
\ln \left( \frac{ \sqrt{x}y^5}{(z+1)^4} \right) &= \ln \left( \sqrt{x}y^5\right) - \ln (z+1)^4\\
&=\ln \left(x^{1/2}y^5\right)-4\ln(z+1)\\
&=\ln x^{1/2}+\ln y^5 -4\ln(z+1)\\
&=\dfrac{1}{2}\ln x+5\ln y -4\ln(z+1)
\end{align*}\]
34. Evaluate \( \sec \dfrac{2\pi}{3} - \tan \dfrac{\pi}{6}.\)
\(\sec \dfrac{2\pi}{3}-\tan \dfrac{\pi}{6} = -2 - \dfrac{1}{\sqrt{3}}\)
35. If we begin with a rectangle with length 5 inches and width 4 inches, then increase the length by \(8 \%\), what is the change in area?
We begin with a rectangle of area \(20\) in\(^2\). If we increase the length by \(8 \%\), then our new length is \(5.4\) inches. This gives a new area of \(21.6\) in\(^2\). This gives a total change in area of \(1.6\) in\(^2\).
36. Evaluate \( f(2)-f(-3)\) given \( f(x)=\left\{ \begin{array}{ll} x^3+1, & x>1\\2x^2-3,&x\leq 1\end{array}\right.\)
\(f(2)=(2)^3+1=9\) and \(f(-3)=2(-3)^2-3=18-3=15\), so \(f(2)-f(-3)=9-15=-6\).
37. Simplify the expression \(\dfrac{\cos^2 (\theta)}{1+\sin(\theta)}.\)
Use the identity \(\cos^2\theta = 1-\sin^2 \theta\) to get
\[\begin{align*}
\frac{\cos^2(\theta)}{1+\sin(\theta)} &= \frac{1-\sin^2\theta}{1+\sin \theta}\\
&=\frac{(1+\sin \theta)(1-\sin \theta)}{1+\sin\theta}\\
&=1-\sin \theta
\end{align*}\]
38. Evaluate \(\log_4\left(\dfrac{1}{\sqrt[3]{16}}\right)\).
\[\begin{align*}
\log_4 \left(\dfrac{1}{\sqrt[3]{16}}\right) &=\log_4\left( \frac{1}{\sqrt[3]{4^2}}\right)\\
&=\log_4 \left( \dfrac{1}{4^{2/3}}\right)\\
&=\log_4 4^{-2/3} \\
&=-\dfrac{2}{3}\\
\end{align*}\]
39. Simplify \(\dfrac{\frac{1}{a}-b}{\frac{1}{b^3}+a}.\)
\(\dfrac{\frac{1}{a}-b}{\frac{1}{b^3}+a} =
\dfrac{\left(\frac{1}{a}-b\right)\left(ab^3\right)}{\left(\frac{1}{b^3}+a\right)\left(ab^3\right)}
=\dfrac{b^3-ab^4}{a+a^2b^3}\)
40. A bacteria culture contains \(1200\) bacteria and doubles every day. How many hours will it take the culture to reach 10000 bacteria?
Use the exponential model \(y(t)=y_0e^{kt}\), where \(y(t)\) is the size of the population at time \(t\) and \(y_0\) is the initial size of the population. We know that \(y_0=1200\), hence \(y(t)=1200e^{kt}\). Since the population doubles everyday, we know
\[\begin{align*}
2400&=1200e^{k\cdot 24}\\
2&=e^{24k}\\
\ln 2&= 24 k\\
k&=\dfrac{1}{24}\ln 2\\
k&= \ln 2^{1/24}\\
\end{align*}\]
Thus, \(y(t)=1200e^{t\ln 2^{1/24}} = 1200 e^{\ln 2^{t/24}}=1200\cdot 2^{t/24}\) (note \(t\) is in hours). Now solve for \(t\) when \(y(t)=10000\)
\[\begin{align*}
10000&=1200\cdot 2^{t/24}\\
\dfrac{10000}{1200}&=2^{t/24}\\
\dfrac{25}{3}&=2^{t/24}\\
\log_2\left(\dfrac{25}{3}\right) &= \dfrac{t}{24}\\
t&=24\log_2 \left(\dfrac{25}{3}\right)\\
\end{align*}\]
So, it will take \(24 \log_2 \left( \dfrac{25}{3}\right)\) hours for the culture to reach \(10,000\) bacteria.
![Accordion CMSUser Widget]()
