Practice Problems for MPE2 for Math 142
To see the main MPE page with a list of resources and information for the MPE, click the following link.
Math Placement Exam
If you would like a paper version of the following problems, you can download them at the following links.
MPE2 for 142 Practice MPE2 for 142 Practice Solutions
Math Placement Exam
If you would like a paper version of the following problems, you can download them at the following links.
MPE2 for 142 Practice MPE2 for 142 Practice Solutions
Directions. The following are review problems for the MPE. We recommend you work the problems yourself, and then click "Reveal Answer" to check your answer. If you do not understand a problem, you can click the "More Examples" link below most problems to see similar questions. While there are no videos for the MPE problems, these similar examples do have videos explaining the solution.
1. Rationalize the denominator. \(\displaystyle \frac{14}{3+\sqrt{2}}\)
2. Find the sum or difference as indicated, and write your answer in simplified form.\[\frac{x+2a-3}{x+a}-\frac{x+6}{2x}\]
3. Factor and reduce to simplest form.\[\frac{6x^2+11xy-10y^2}{3x^2+10xy-8y^2}\]
4. Solve the following equation: \(5(x-7)-13(x-7)-6=0.\)
5. Find the point \((x,y)\) which satisfies both equations. What is the value of \(x+y\)?\[\begin{align*} -2x+4y&=12\\ 3x-5y&=-3\end{align*}\]
6. Two investments are made, totaling \($10,000\). In one year, these investments yield \($650\) in simple interest. Part of the \($10,000\) is invested at \(5\frac{1}{2}\%\), and the rest at \(6\frac{3}{4}\%\). How much more money is invested at \(6\frac{3}{4}\%\)?
7. Given the linear equation \(2ax + 3by = 7c\), where \(a\), \(b\) and \(c > 0\), if \(x\) decreases by \(10\) units, what is the corresponding change in \(y\)?
8. Perform the indicated operations and simplify. \[\frac{8}{x+1}-\left(\frac{y}{z+2} \div \frac{y-4}{w}\right)\]
9. Find the equation of the line passing through the point \((5,1)\) with a slope of 7. Use the equation you find to determine the value of \(y\) when \(x=-4.\)
10. Line \(A\) passes through the points \((2k+3, 4k−6)\) and \((−2, 16)\). Find the value of \(k\) if line \(A\) has a slope of \(0\).
11. Beginning with the function \(f(x)=\sqrt{x}\), find the function \(g(x)\) that shows \(f(x)\) shifted left 2 units, reflected about the \(x\)-axis, and then shifted up 7 units.
12. Solve for \(x\) in the inequality \[x+2-(5x-10)\geq 3\]
13. Find the domain of \[f(x)=\dfrac{x^2-3x-2}{6x^2-54}\]
14. Find the domain of the function below. \[f(x)=\left\{\begin{array}{cc}\dfrac{2x^2+13}{x^2-1}, & x<0\\ \dfrac{5x-26}{x+2}, & x\geq 0\end{array} \right.\]
15. Find the \(x\)- and \(y\)-intercept(s) of the function \(2x+3y=10\), if any exist.
16. Simplify the expression and then write your answer using positive rational exponents. \[ \left(\dfrac{2}{\sqrt{x^5}}\right) \left(\sqrt[3]{4x}\right)\]
17. If we begin with the graph of \(f(x) = x^2\) and shift \(f (x)\) 4 units to the right, shrink f (x) vertically by a factor of \(\frac{1}{2}\), and then shift \(f(x)\) upward 10 units, write the equation for the transformed graph.
18. Find \(f\circ g\) (also denoted \(f(g(x))\)) if \(f(x)=\dfrac{x}{x+1}\) and \(g(x)=\dfrac{2}{x}\). Simplify.
19. Write the following inequalities in interval notation.
- \(x\geq 2\)
- \(-4\leq x < 7\)
- \(x<-5\)
- All \(x\) such that \(x\) is a real number.
20. Write the following intervals using inequality notation.
- \([0,2)\)
- \((-\infty,4)\)
- \([7,\infty)\)
21. If \(f(x)=\sqrt{x+4}\), find and simplify \(\dfrac{f(2+h)-f(2)}{h}.\)
22. Perform the operations indicated and simplify.\[\frac{x^2}{x^2-x-2}-\frac{4}{x^2+x-6}+\frac{x}{x^2+4x+3}\]
23. Evaluate \( f(2)-f(-3)\) given \( f(x)=\left\{ \begin{array}{ll} x^3+1, & x>1\\2x^2-3,&x\leq 1\end{array}\right.\)
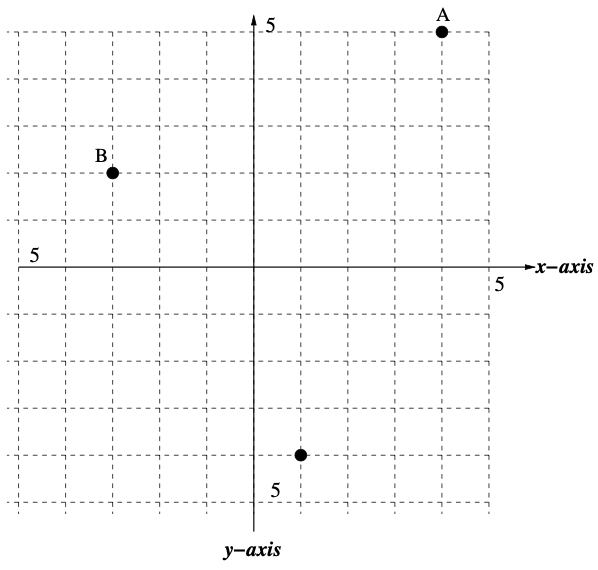
24. Given the points \(A(4,5)\), \(B(-3,2)\), and \(C(1,-4)\), do the following:
- Plot points \(A\), \(B\), and \(C.\)
- Find the equations of the horizontal line going through the point \(B.\)
- Find the equation of the vertical line going through point \(C.\)
- Find the equation of the line containing points \(A\) and \(C\) and write the equation in point-slope form.
- Find an equation of the line that contains point \(B\), but is perpendicular to the line containing points \(A\) and \(C\).
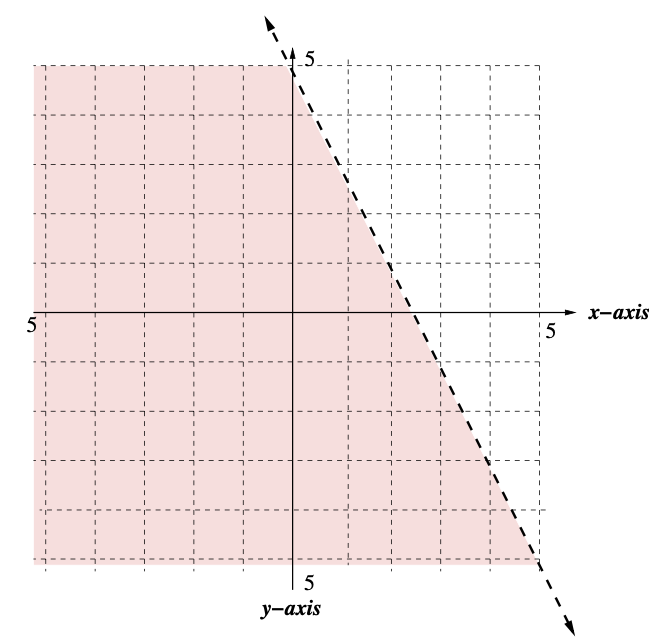
25. Graph the inequality \(4x+2y \leq 10\). Does the point \( \left( -3, \dfrac{8}{3}\right)\) lie in the solution set?
26. Simplify the following expressions
- \(\dfrac{2x}{xy+xz+5x}\)
- \(\dfrac{(2.4)(.4)}{(2.5)(.4)+(.6)(.4)+(1.9)(.4)}\)
27. Russ set up a lemonade stand where he sold 16 ounce cups of freshly squeezed lemonade for $2 per cup. It cost Russ $0.25 in supplies (lemons, sugar, water, paper cups, and ice) to make each cup of lemonade, and he spent a total of $52.50 on other necessary supplies (e.g., table, lemonade dispenser, signs). If \(x\) is the number of cups of lemonade that Russ makes and sells on the day of the lemonade stand, find the following:
- The cost function, \(C(x)\), to make \(x\) cups of lemonade.
- The revenue function, \(R(x)\), generated from selling \(x\) cups of lemonade.
- The profit function, \(P(x)\), made from selling \(x\) cups of lemonade.
- How many cups of lemonade must Russ sell to break even on his lemonade stand?
28. Find the roots of the function \(f(x)=3x^2+7x-2.\)
29. There are 5 white balls, 8 red balls, 7 yellow balls, and 4 green balls in a container. A ball is chosen at random. What is the probability a red ball is chosen?
30. Sue has 7 different books to put on a shelf. How many different ways can she arrange the books on the shelf?
31. Jay wants to make a box, with no lid (or top), out of a \(10'' \times 6''\) rectangular piece of cardboard. If Jay cuts squares with dimensions \(x\) by \(x\) out of each corner of the cardboard, and then folds up the corners to make an open box, find a function that represents:
- The volume of the box.
- The surface area of the box.
32. A classroom of 100 students has 65 females, 10 seniors, and 6 females who are seniors. How many students in this classroom are not female and also not a senior?
33. When making his 6-period class schedule, Mark has 2 options of classes to take for first period, 4 options for second period, 1 option for third period, 1 option for fourth period, 3 options for fifth period, and 5 options for sixth period. How many different schedules can Mark possibly have if he takes one class per period?
34. Suppose an object is moving at 66 feet per second. How fast, in miles per hour, would a car have to travel to keep pace with this object?