Coterminal and Reference Angles
Instructions
- The first videos below explain the concepts in this section.
- This page includes exercises that you should attempt to solve yourself. You can check your answers and watch the videos explaining how to solve the exercises.
Concepts
- Draw angles in standard position
- Defining coterminal angles
- Calculate negative and positive coterminal angles
- Locating and calculating the measure of referene angles
Exercises
Directions: You should attempt to solve the problems first and then watch the video to see the solution.
1. Find one negative and one positive coterminal angle for \(60^\circ\) and \(\dfrac{\pi}{3}.\)
2. Draw an angle of \(120^\circ\) in standard position and find its reference angle.
3. Draw an angle of \(\dfrac{7\pi}{4}\) in standard position and find its reference angle.
4. Find an angle between 0 and \(2\pi\) that is coterminal to \(\dfrac{19\pi}{6}.\) Then draw the angle in standard position and find its reference angle.
5. Find an angle between \(0^\circ\) and \(360^\circ\) that is coterminal to \(-660^\circ\). Then draw the angle in standard position and find its reference angle.
Next Section
If you are working through the Algebra Series in order, then you should visit the following section next.
Pick Another Section
If you are studying just the topics you need, you can pick a different section to study from the graph below. You are currently in the highlighted section.
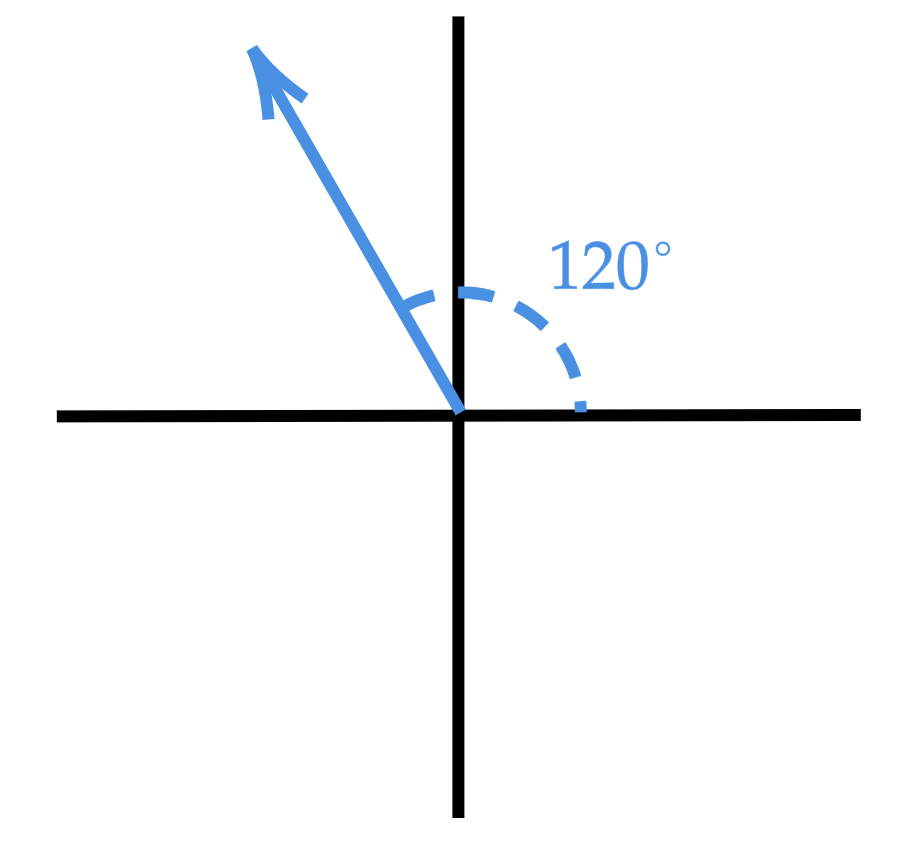 Solution Method: First, to draw the angle in standard position we need to place its vertex on the origin, and its initial side on the positive x-axis. Then we just determine where the terminal side needs to be. The \(120^\circ\) angle is positive so it's measured counterclockwise from the initial side. Each quadrant is \(90^\circ\) so \(120^\circ\) will lie 30 degrees inside quadrant 2.
Solution Method: First, to draw the angle in standard position we need to place its vertex on the origin, and its initial side on the positive x-axis. Then we just determine where the terminal side needs to be. The \(120^\circ\) angle is positive so it's measured counterclockwise from the initial side. Each quadrant is \(90^\circ\) so \(120^\circ\) will lie 30 degrees inside quadrant 2.