Increasing/Decreasing Functions, Concavity, Local Extrema and Absolute Extrema
Instructions
- First, you should watch the concept videos below explaining the topics in the section.
- Next, you should attempt to solve the exercises. You can check your answers and watch videos explaining the exercises.
- When you have finished the material below, you can start on the next section or return to the main workshop page.
Concepts
- Using the first derivative to determine where a function is increasing and decreasing
- Using the First Derivative Test to find the local maximums and local minimums of a function
- Using the second derivative to determine where a function is concave upward and concave downward and to find all inflection points
- Using the Second Derivative Test to find the local maximums and local minimums of a function
Exercises
Directions: You should attempt to solve the problems first and then watch the video to see the solution.
1. Find the critical values of the following functions, if they exist.
- \(f(x)+x^5-5x^4-20x^3+100\)
- \(f(x)=\dfrac{x^3}{x^2-9}\)
2. Find the intervals where \(f(x)=\dfrac{1}{(x-4)^2}\) is increasing/decreasing.
3. For the following function, find the critical values of the function, intervals where the function is increasing/decreasing, and the local extrema of the the function as well as where they occur.
\[f(x)=x^3-6x^2+9x+2\]
\[f(x)=x^3-6x^2+9x+2\]
4. An office supply company sells external web cameras. The price-demand function for the web cameras is \(p(x)=-0.2x+56,\) where \(p(x)\) is the price, in dollars, per camera when \(x\) web cameras are purchased. Find the intervals where the company's revenue function, \(R,\) is increasing/decreasing as well as the local extrema of the revenue function, assuming \(R(x)\) is the company's revenue, in dollars, when \(x\) web cameras are sold.
5. Find the intervals of concavity and any inflection points of the following function.
\[f(x)=e^{2x}-e^{-2x}\]
\[f(x)=e^{2x}-e^{-2x}\]
6. Given the graph of \(f'\) shown below and that \(f\) and that \(f\) is continuous on its domain of \((-\infty,7)\cup (7,\infty),\) find the partition numbers of \(f'',\) the intervals of concavity of \(f,\) and the \(x\)-values of any inflection points of \(f.\)
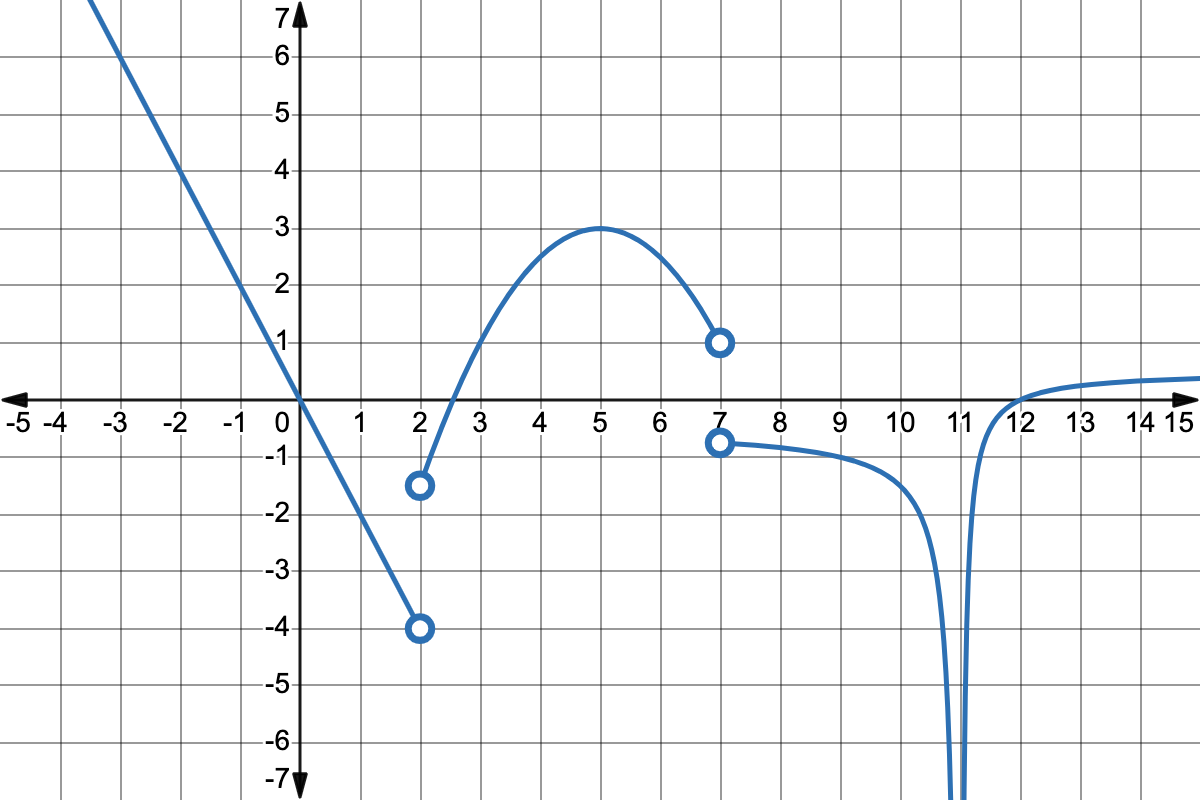

7. Use the Second Derivative Test, if possible, to find any local extrema of the following function. If it is not possible, explain why.
\[f(x)=\frac{100}{x}+x\]
\[f(x)=\frac{100}{x}+x\]