Trigonometric Functions With the Unit Circle
Instructions
- The first videos below explain the concepts in this section.
- This page includes exercises that you should attempt to solve yourself. You can check your answers and watch the videos explaining how to solve the exercises.
Concepts
- Using the unit circle to determine exact values of trigonometric functions at special angles
- Relating the coordinates of points on the unit circle with the cosine and sine of the special central angles
- Using coterminal angles and the unit circle to determine exact values of trigonometric functions at negative angles and angles greater than 360 degrees (or 2 pi)
- Utilize knowledge of the unit circle to solve trigonometric equations
- Determine the sign of sine, cosine, and tangent ratios in each quadrant of the Cartesian plane
Exercises
Directions: You should attempt to solve the problems first and then watch the video to see the solution.
1. Find the exact values of \(\tan\left(\dfrac{3\pi}{4}\right),\) \(\tan(210^\circ),\) and \(\tan(\pi).\)
2. Find the exact values of \(\csc\left(\dfrac{11\pi}{6}\right),\) \(\sec\left(45^\circ\right),\) and \(\cot\left(\dfrac{5\pi}{3}\right).\)
3. Find the exact value of \(\cos(5\pi)\) and \(\cot(480^\circ).\)
4. Find the exact value of \(\sin(-45^\circ)\) and \(\sec\left(-\dfrac{2\pi}{3}\right).\)
5. Find all \(0 \leq \theta \leq 2\pi\) satisfying \(\sin{\theta}=\dfrac{\sqrt{3}}{2}.\)
6. Find all \(0^\circ \leq \theta \leq 360^\circ\) satisfying \(\sec{\theta}=-\sqrt{2}\) and \(\tan{\theta}>0.\)
Next Section
If you are working through the Algebra Series in order, then you should visit the following section next.
Pick Another Section
If you are studying just the topics you need, you can pick a different section to study from the graph below. You are currently in the highlighted section.
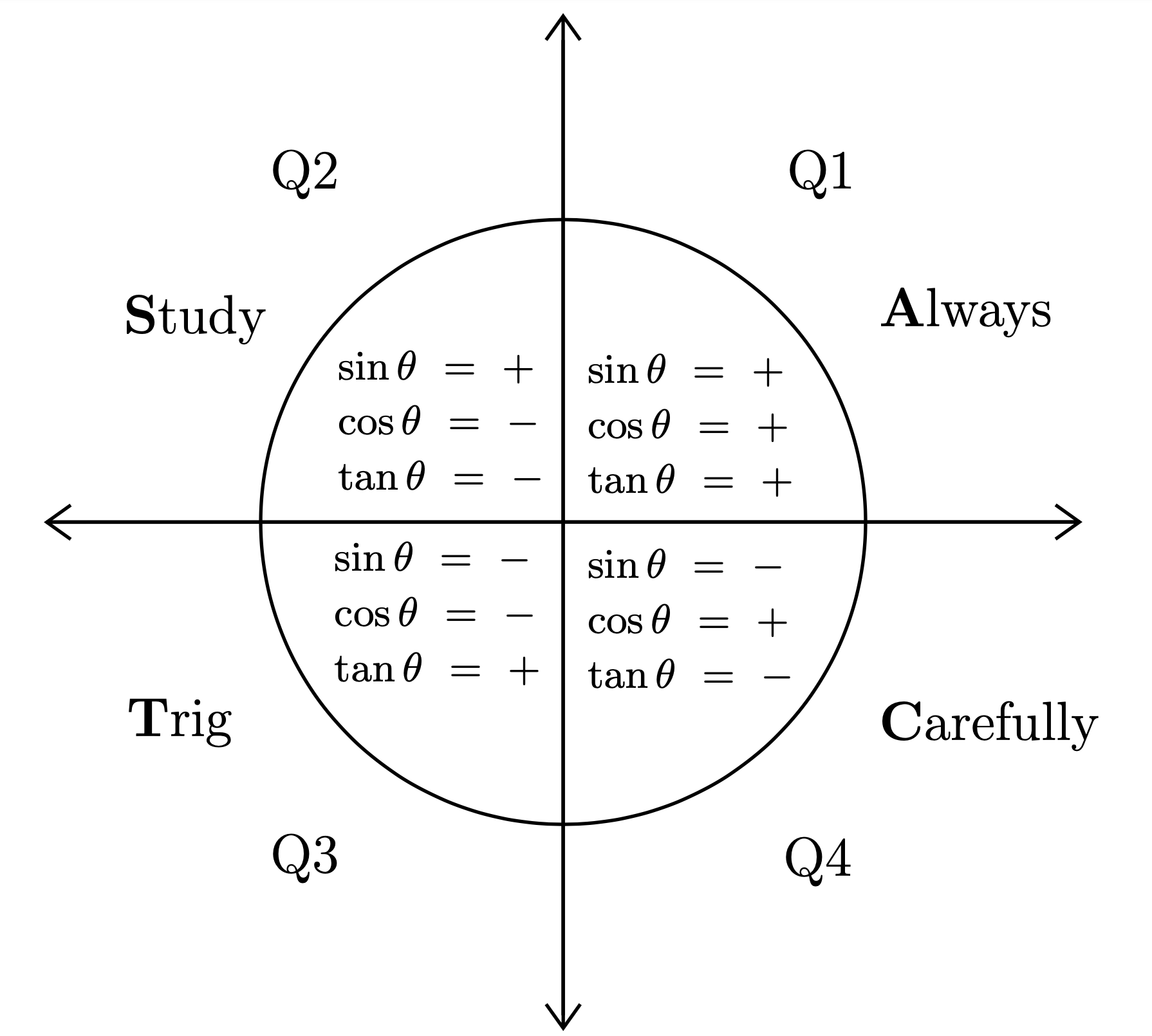 First, we're going to look at the trig function and its sign. Each trig function is only positive in two quadrants on the unit circle, and negative in the other two. To help us remember which quadrants each trig function is positive in, we use the acronym ASTC, Always-Study-Trig-Carefully. You may have heard it before as All-Students-Take-Calculus or Add-Sugar-To-Coffee, use whatever works for you. In the first quadrant, all three (sin, cosine, and tangent) are positive. In the second quadrant, sine is positive and cosine and tangent are negative, in the third tangent is positive (because negative divided by negative is positive), and in the fourth quadrant cosine is positive.
First, we're going to look at the trig function and its sign. Each trig function is only positive in two quadrants on the unit circle, and negative in the other two. To help us remember which quadrants each trig function is positive in, we use the acronym ASTC, Always-Study-Trig-Carefully. You may have heard it before as All-Students-Take-Calculus or Add-Sugar-To-Coffee, use whatever works for you. In the first quadrant, all three (sin, cosine, and tangent) are positive. In the second quadrant, sine is positive and cosine and tangent are negative, in the third tangent is positive (because negative divided by negative is positive), and in the fourth quadrant cosine is positive.