
Quadratic Equations Video 1
Explaining the standard form for a quadratic equation and the possible number of solutions
Problem: Show the quadratic equation \(3x^2-x+7=0\) does not have a real solution. Explain why.

Explaining the standard form for a quadratic equation and the possible number of solutions

Solving quadratic equations with the quadratic formula and discussing the number of possible solutions

Solving an equation that contains rational expressions

Solving an equation that contains rational expressions
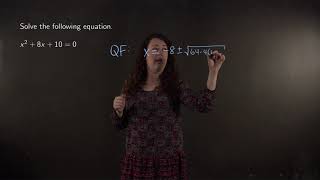
Solving a quadratic equation using the quadratic formula

Solving an equation using the quadratic formula
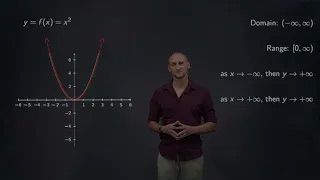
Explaining the graph and properties for the parent function of quadratics

Solving quadratic equations with the difference of two squares formula

Solving quadratic equations by factoring

Solving a quadratic equation by factoring

Solving a quadratic equation by factoring
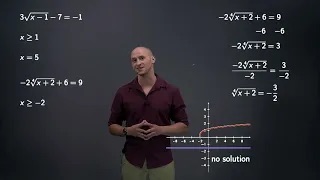
Solving equations with even roots and checking the solutions

Explaining how to solve equations with power and exponential terms
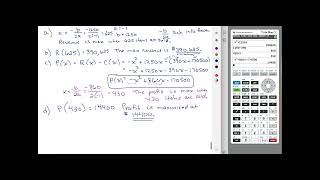
Finding the maximum revenue, maximum profit, and break even quantity for given revenue and cost functions

Solving an equation with exponential functions
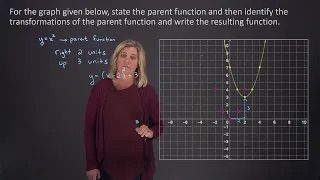
Identifying the parent function and transformations for a given graph
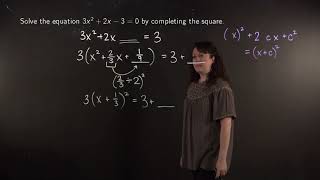
Solving a quadratic equation by completing the square

Solving a trigonometric equation by factoring

Solving a trigonometric equation

Review of limits, continuity, and the Intermediate Value Theorem

Review of the limit definition of a derivative and calculating the derivative

Review of the limit definition of a derivative and calculating the derivative

Continuity of Functions and the Intermediate Value Theorem

Review of the limit definition of a derivative and calculating the derivative

Differentials, linear approximations and quadratic approximations

Review of the limit definition of a derivative and calculating the derivative

Explaining all four cases of partial fraction decomposition

Review of limits, continuity, and the Intermediate Value Theorem

Review of the limit definition of a derivative and calculating the derivative

Review of the limit definition of a derivative and calculating the derivative

Continuity of Functions and the Intermediate Value Theorem

Review of the limit definition of a derivative and calculating the derivative

Differentials, linear approximations, and quadratic approximations

Review of the limit definition of a derivative and calculating the derivative

Explaining all four cases of partial fraction decomposition

Finding the domain of a function with a natural logarithm and denominator

Solving a linear equation algebraically and showing how this relates to the graph
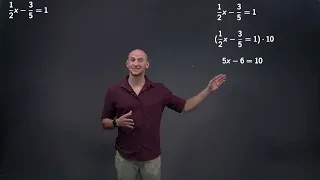
Solving a linear equation algebraically

Solving a linear equation algebraically and showing how this relates to the graph

Explaining the format and possible solutions for a system of two linear equations

Solving a system of two linear equations using a TI-84 calculator

Solving a system of two linear equations using a TI-84 calculator

Discussing how to write the equation of a line through two given points

Discussing properties of quadratic functions including the vertex, domain, range, and end behavior

Explaining how to solve radical equations and then solving example problems
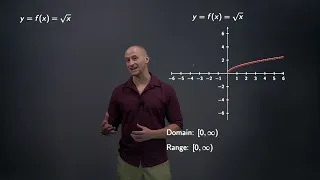
Explaining the general properties of even and odd root functions

Solving equations with odd radicals

Solving equations with multiple radicals

Properties of exponential growth and decay functions

Properties of the exponential function with base e
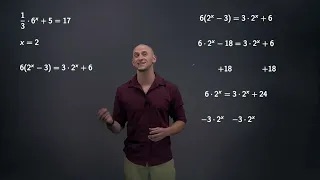
Solving equations with exponential terms

Solving equations with base e exponential terms

Explaining how to solve logarithmic equations

Solving logarithmic equations with a single logarithm term

Solving logarithmic equations with multiple logarithm terms

Solving logarithmic equations with multiple logarithm terms on both sides
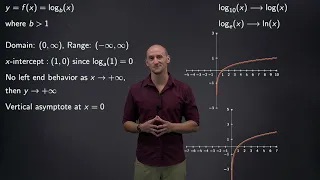
Explaining the basic properties of logarithmic functions

Solving equations that contain rational expressions
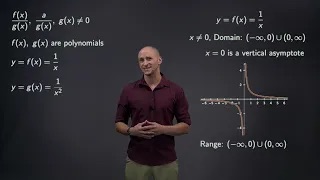
Discussing parent functions of rational functions and their properties

Explaining all four cases of partial fraction decomposition

Explaining the format and possible solutions for a system of two linear equations
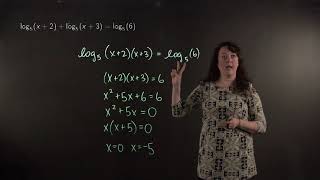
Solving an equation with logarithmic functions

Solving an equation with logarithmic functions

Solving an equation with logarithmic functions

Using the quadratic formula to find the roots of a function

Finding the roots of a cubic polynomial
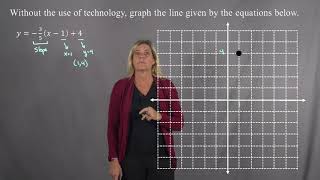
Graphing a line without using technology

Graphing a line without using technology

Graphing a line without using technology

Writing a function for the value of an item depreciating linearly over time
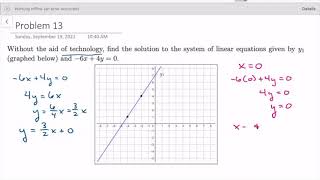
Finding the solution to a system of linear equations by graphing

Graphing the solution set of an inequality with two variables

Graphing the solution set of an inequality with two variables

Graphing the solution set of system of linear inequalities

Explaining how to graph linear inequalities

Graphing two linear inequalities

Sketching the solution set and finding the corner points for a system of linear inequalities

Using a graph to find specific values of a function

Identifying quadratic functions and their properties
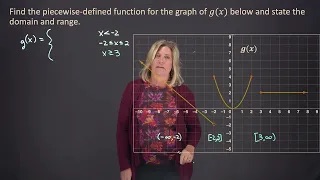
Finding the piecewise-defined function for a given graph along with its domain and range

Graphing a piecewise function
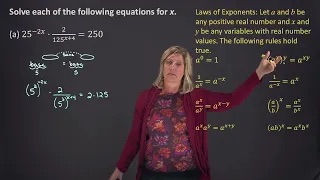
Solving an equation with exponential functions

Identifying the parent function and transformations for a given graph

Drawing the graph of a transformed function given the original graph

Evaluating compositions of two given functions and the graph of a third function
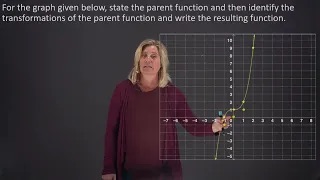
Identifying the parent function and transformations for a given graph
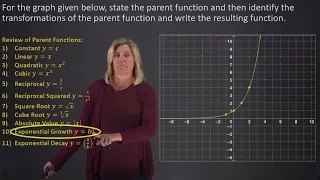
Identifying the parent function and transformations for a given graph

Using the Horizontal Line Test to determine if graphs represent invertible functions

Solving an equation an exponential function

Solving an equation with exponential functions

Solving an equation with a logarithmic function

Solving an equation with several logarithmic functions

Finding the difference quotient for a quadratic function

Finding limits from the graph of a piecewise function

Determining where a piecewise function is continuous from its graph

Determining where the derivative of a function does not exist from a graph

Explaining the Intermediate Value Theorem and the Bisection Method

Using the Intermediate Value Theorem and Bisection Method to approximate the solution of an equation

Explaining the definition of logarithmic scale and double-log plots

Explaining the logarithmic scale and a semilog plot

Using logarithms to transform a power function into a linear function

Using logarithms to transform an exponential function to a linear function

Explaining the Sandwich (or Squeeze) Theorem with a graphical example

Solving a limit at infinity using the Sandwich (or Squeeze) Theorem

Factoring a quadratic

Factoring a polynomial

Factoring a quadratic

Dividing rational expressions and simplifying

Subtracting rational expressions and simplifying

Performing operations with rational expressions and simplifying
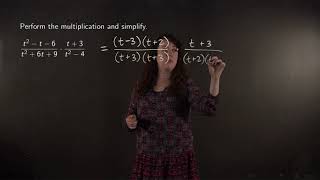
Performing operations with rational expressions and simplifying

Solving a polynomial equation using factoring by grouping

Determining if an equation represents a function
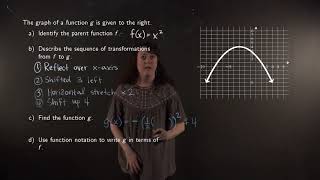
Identifying the parent function and transformations of a function
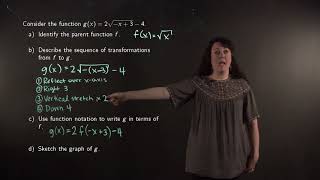
Identifying the parent function and transformations of a function

Putting a quadratic function in standard form and determining its properties

Putting a quadratic function in standard form and determining its properties

Finding the x-intercepts of quadratic functions
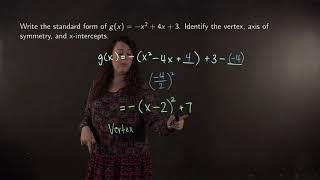
Putting a quadratic function in standard form and determining its properties

Finding the end behavior of a polynomial

Finding properties of a polynomial including zeros and end behavior

Determining the properties of a rational function and graphing it
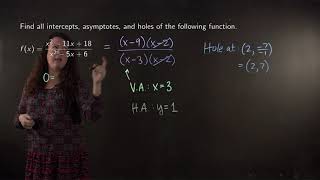
Determining the properties of a rational function and graphing it

Solving a nonlinear inequality

Solving a nonlinear inequality

Solving a nonlinear inequality

Graphically verifying if two functions are inverses

Restricting the domain of a function so it is one-to-one and has an inverse

Determining algebraically the inverse of a function

Determining algebraically the inverse of a function

Determining algebraically the inverse of a function
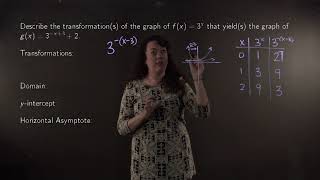
Determining properties of an exponential function

Determining properties of an exponential function
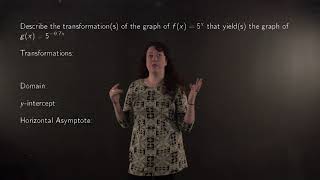
Determining properties of an exponential function
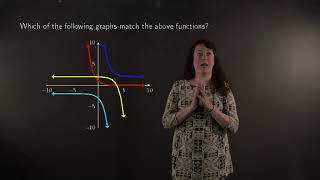
Identifying the graph of an exponential function

Solving an equation with an exponential function

Determining properties of an exponential function
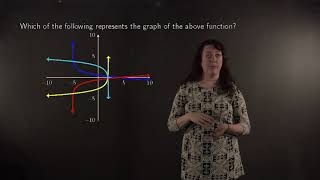
Determining the graph of a logarithmic function

Determining the graph of a logarithmic function

Solving an equation with an exponential function

Solving an equation with an exponential function

Solving an equation with an exponential function

Solving an equation with exponential functions by factoring

Modeling a population size with an exponential function

Determining the properties of a sine function and graphing it

Determining the properties of a cosine function and graphing it

Writing the equation for a sine function to match a given graph

Writing the equation for a cosine function to match a given graph

Solving a trigonometric equation

Solving a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Using double angle formulas to evaluate trigonometric functions

Adding and subtracting vectors graphically

Finding the properties of a transformed tangent function and graphing it

Using a graph to evaluate a function

Determining if a function is even or odd

Derivatives and vectors with some physics applications

Review of derivatives and tangent lines to functions and vector equations
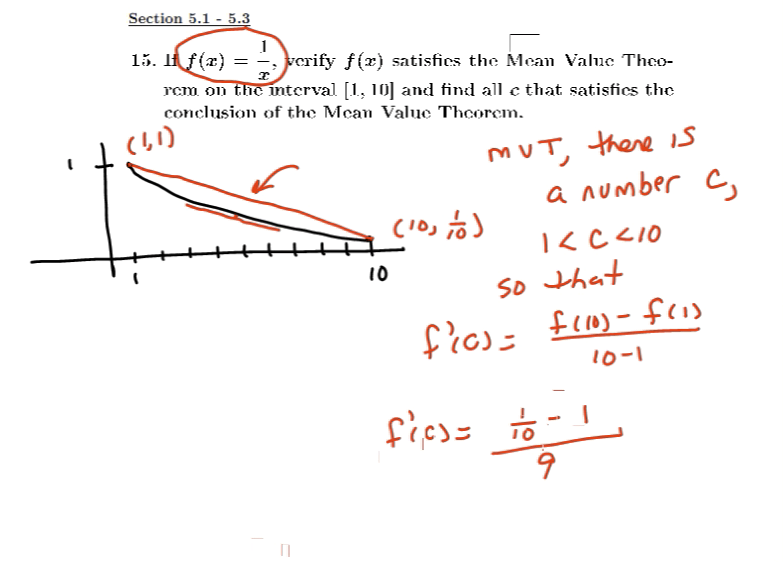
Mean Value Theorem and using derivatives to find the shape of curves

Properties and derivatives of inverse trigonometric functions

Evaluating limits of functions

Evaluating Limits of Functions
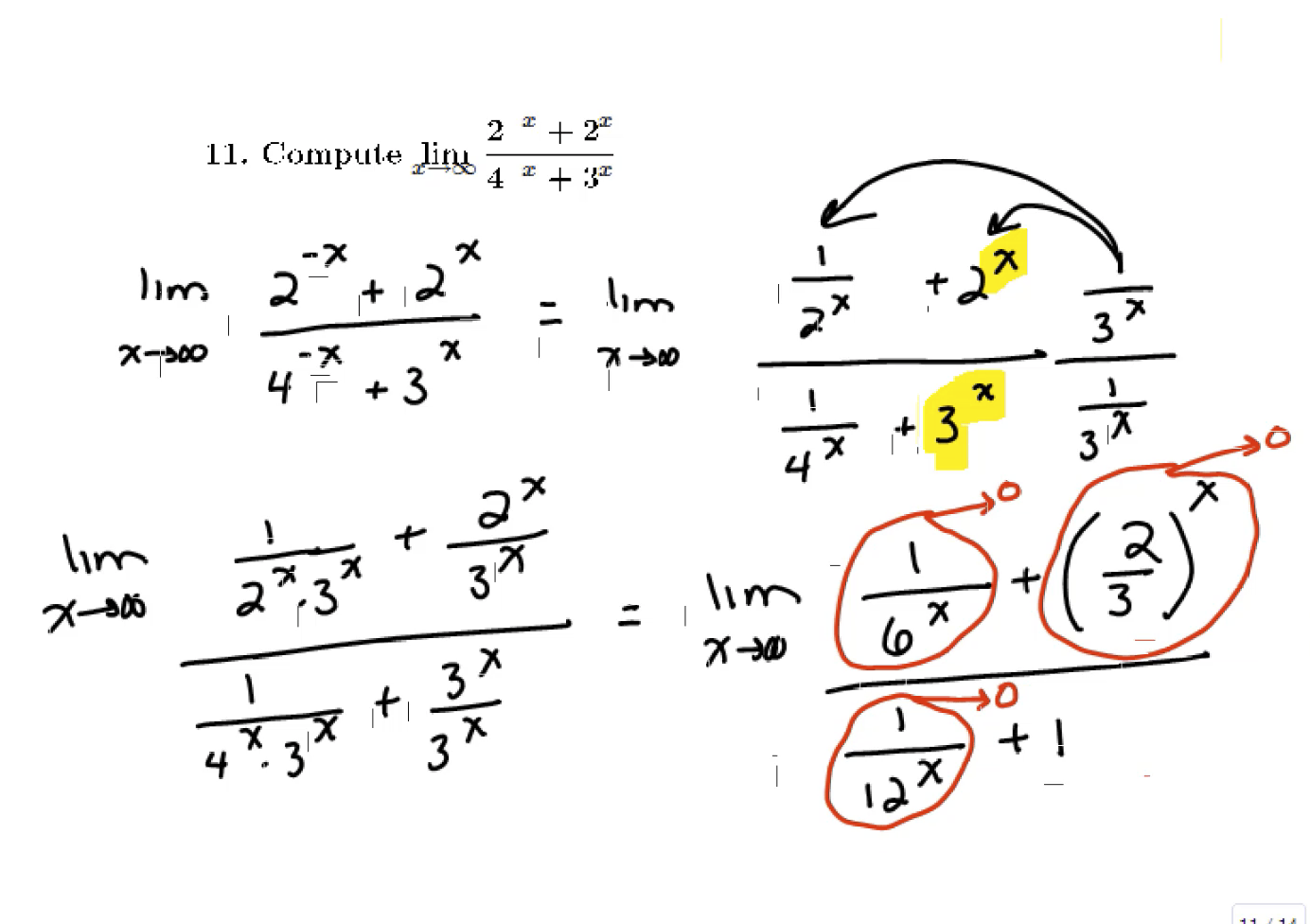
Approximation and Newton's Method, and limits and derivatives of exponential functions

Review of derivatives and tangent lines to functions and vector equations

Derivatives and tangents to curves
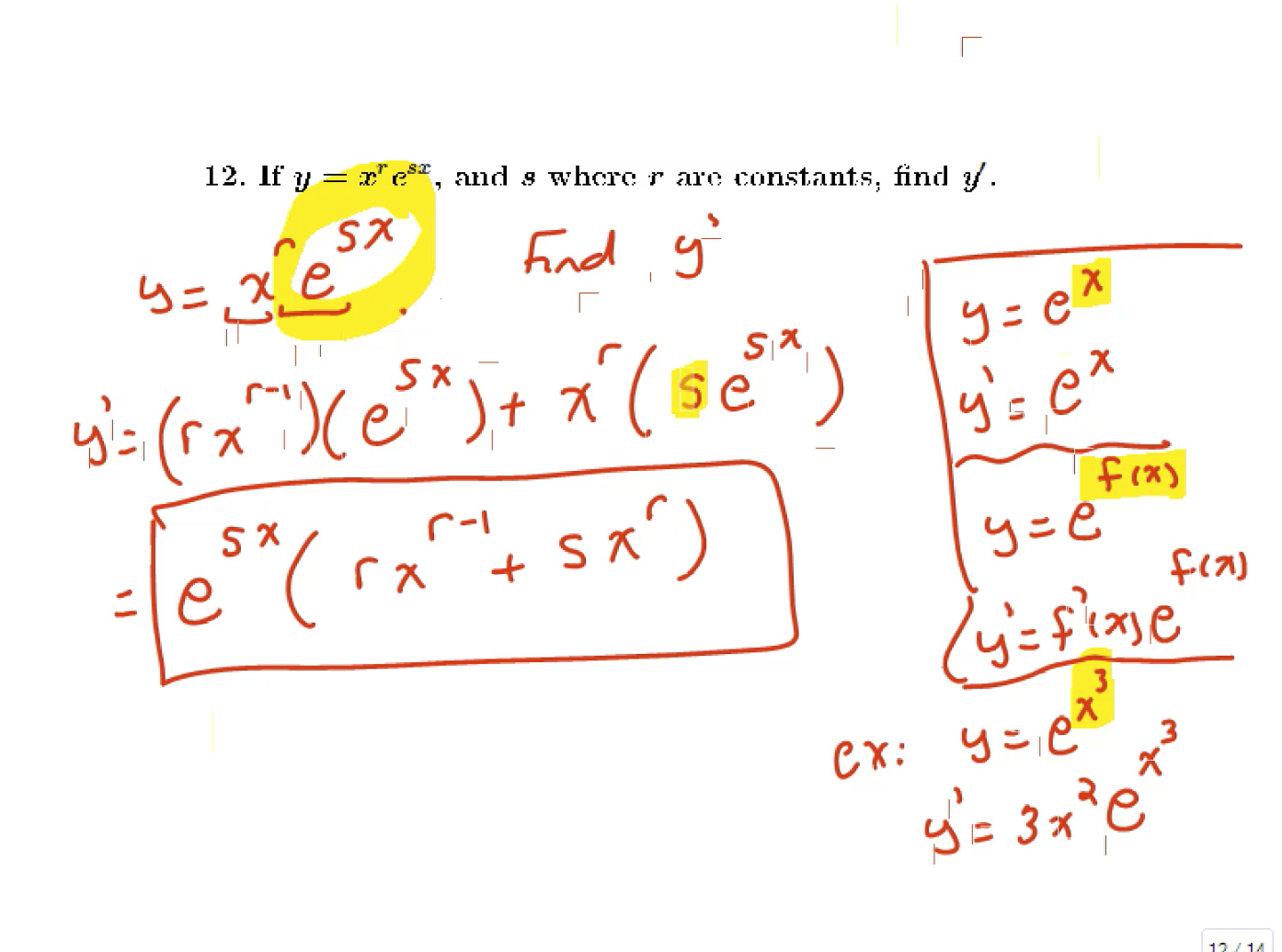
Approximation and Newton's Method, and limits and derivatives of exponential functions

Derivatives and vectors with some physics applications

Properties and derivatives of inverse trigonometric functions

Derivatives and vectors with some physics applications

Using derivatives to find properties of graphs
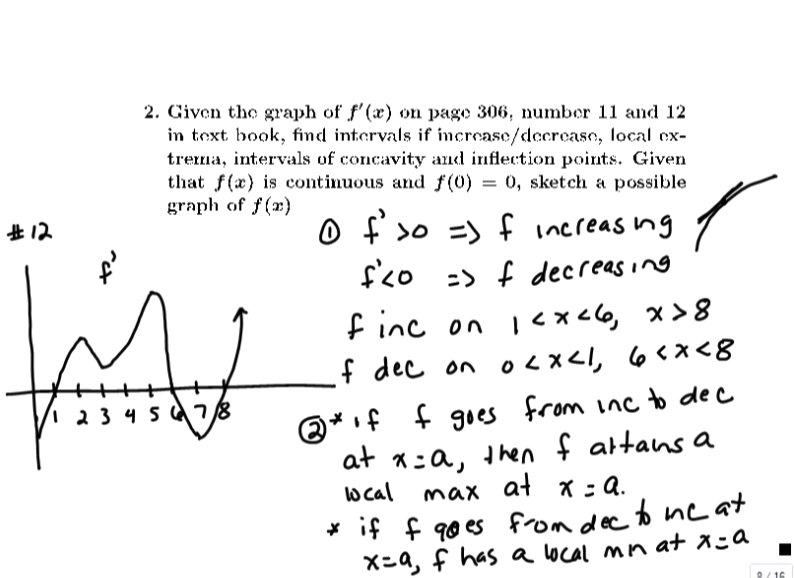
Using derivatives to find properties of graphs

Converting parametric equations into a Cartesian equation and graphing

Finding a Cartesian equation for a parametric equation and graphing it

Find the Cartesian form and sketch the graph for the parametric equation of a line

Using the graph of a function to sketch a graph of its derivative

Finding the derivatives of compositions of functions from their graphs

Determining the properties of a function from the graph of its derivative

Review of work and average value

Converting parametric equations into a Cartesian equation and graphing

Converting parametric equations into a Cartesian equation and graphing

Converting parametric equations into a Cartesian equation and graphing

Converting parametric equations into a Cartesian equation and graphing

Finding the area of a region bounded by two curves
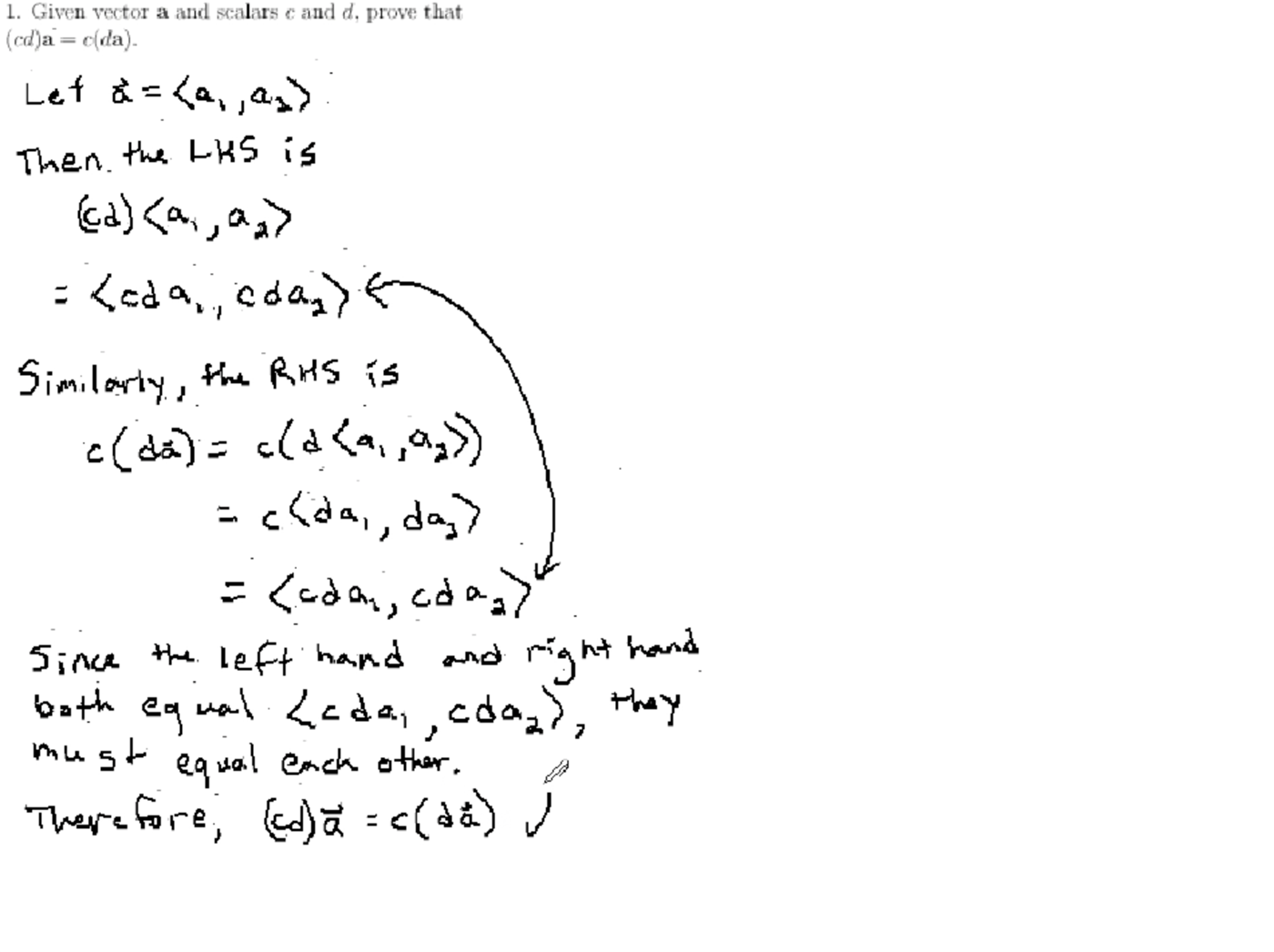
Proving associative and scalar multiplication properties for vectors

Proving facts about the derivatives of vector functions including the product rule

Derivatives and vectors with some physics applications

Derivatives and vectors with some physics applications
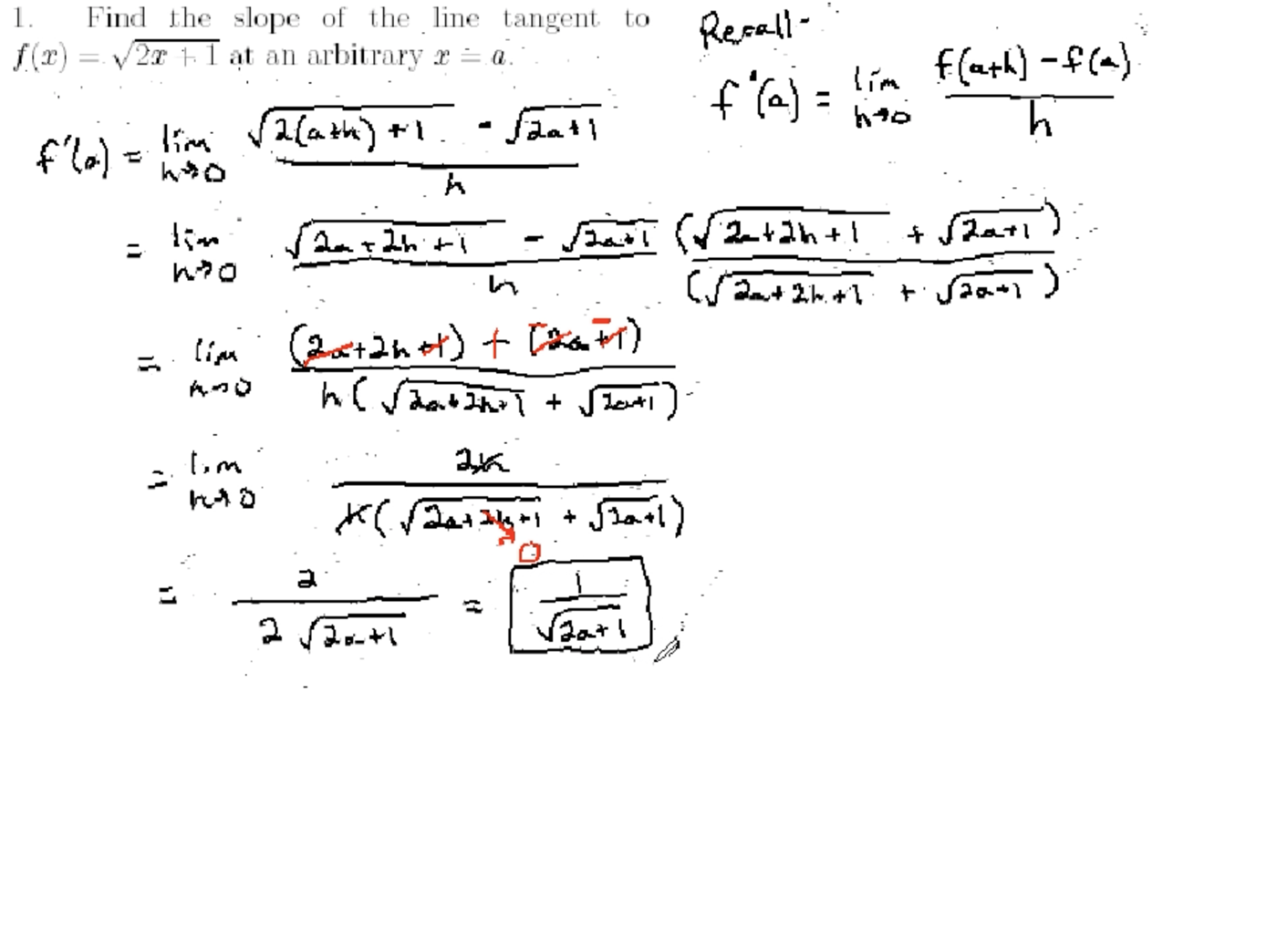
Using the limit definition to find derivatives of functions and vector functions

Review of derivatives and tangent lines to functions and vector equations

Mean Value Theorem and using derivatives to find the shape of curves

Properties of inverse trig functions and the derivative of arctangent

Properties and derivatives of inverse trigonometric functions

Evaluating limits of functions

Evaluating limits of functions and using the Squeeze Theorem

Proving a piecewise function and a polynomial are continuous

Approximation and Newton's Method, and limits and derivatives of exponential functions

Using the limit definition to find derivatives of functions and vector functions

Using the limit definition to find derivatives of functions and vector functions

Review of derivatives and tangent lines to functions and vector equations

Review of derivatives and tangent lines to functions and vector equations
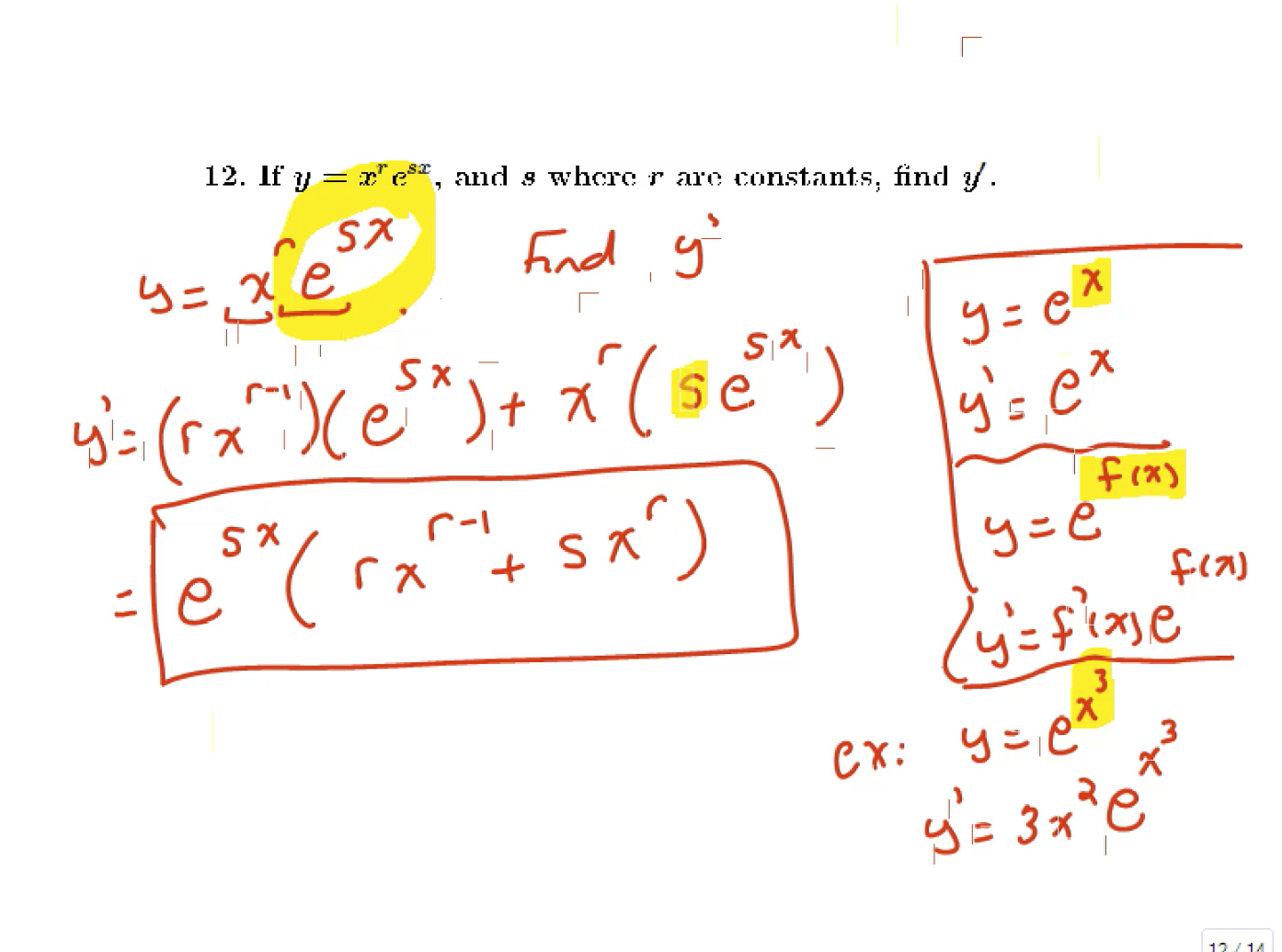
Approximation and Newton's Method, and limits and derivatives of exponential functions

Derivatives and vectors with some physics applications

Properties and derivatives of inverse trigonometric functions

Properties of inverse trig functions and the derivative of arctangent

Using derivatives to find properties of graphs

What the derivatives of a function tell us about the shape of its graph

Using derivatives to find properties of graphs

Proving L'Hospital's Rule and using it to evaluate limits

Optimizing values in word problems

Proving and then applying the Fundamental Theorem of Calculus

Review of work and average value

Using integrals to solve work problems and find the average value

Showing how an equation in three dimensional space represents a plane
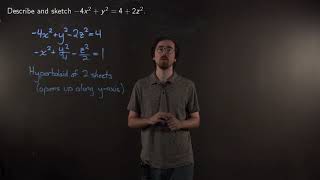
Identifying the equation of a hyperboloid and sketching its graph

Identifying the equation of a cone in three dimensions and sketching its graph

Finding and sketching the domain of a function of two variables

Finding and sketching the domain of a function of two variables

Sketching the graph of a function of two variables

Sketching the graph of a function of two variables

Sketching the level curves of a function of two variables

Sketching the level curves of a function of two variables

Describing the level surfaces of a function of three variables

Evaluating a double integral over a given region

Evaluating a double integral over a given region

Evaluating a double integral and sketching the region of integration

Changing the order of integration for a double integral

Evaluating a double integral by reversing the order of integration

Setting up double integrals of Type I and II to give the volume of a solid under a surface

Evaluating a double integral over a circular region by changing to polar coordinates

Evaluating a double integral by changing to polar coordinates

Evaluating a double integral by changing to polar coordinates

Converting a double integral to a double integral in polar coordinates

Writing an iterated integral in polar coordinates that gives the volume of the solid that lies below a paraboloid

Writing an iterated integral in polar coordinates that gives the volume of the solid bounded by a cone

Writing an a triple integral over a given solid as an iterated integral

Evaluating a triple integral over a solid bounded by given surfaces

Writing an iterated integral that gives the volume of a solid

Evaluating a triple integral over a solid bounded by elliptic paraboloids

Writing a triple integral as an iterated integral in cylindrical coordinates

Converting an iterated triple integral into cylindrical and spherical coordinates

Using an iterated integral in spherical coordinates to find the volume of a solid

Evaluating a triple integral for a given solid by writing an iterated integral in spherical coordinates

Using Python to find the equation of the tangent line to a curve and graphing the result

Using Python to plot an implicit curve and find a tangent line using implicit differentiation

Using Python to numerically estimate a limit, graphically estimate a limit, and find the exact limit

Using Python to find the tangent line to a parametric equation and plot the two graphs

Graphing a piecewise function using Python

Solving a multistep word problem in Python and graphing the resulting function

Evaluating iterated integrals over the same region but with different orders of integration

Writing and then solving an iterated integral for a given region

Using double integrals to calculate the weight of a plate given its density and size

Finding the domain of a function with a denominator, square root, and logarithm

Finding the domain of a function with a square root in the denominator

Finding the domain of a function with a root and a logarithm in the denominator
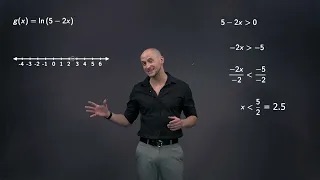
Finding the domain of a logarithmic function
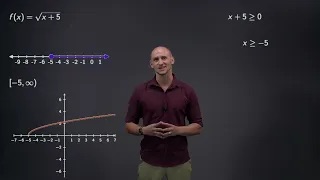
Finding the domain of even and odd roots
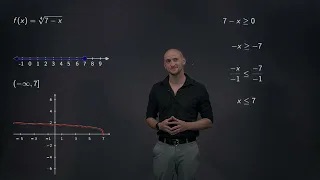
Finding the domain of functions with even and odd roots

Finding the domain of several rational functions
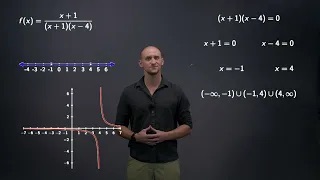
Finding the domain of a rational function

Explaining how to find any holes and vertical asymptotes of a rational function
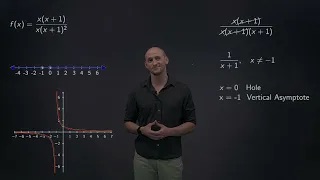
Finding the domain of a rational function using factoring

Explaining domain restrictions for denominators, even roots, and logarithms

Explaining the main three forms for linear equations
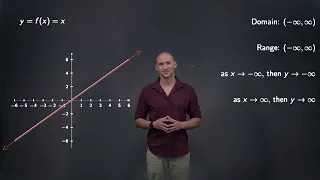
Discussing properties of linear functions

Discussing the types of linear graphs including horizontal and vertical lines and their properties

Writing a linear equation of profit from a business word problem

Solving a system of linear equations with two variables

Solving a system of two linear equations with two variables using the elimination method

Solving a system of two linear equations using a TI-84 calculator

How to rewrite radical terms as power terms

Simplifying power and exponential expressions using properties of exponents

Simplifying power and exponential expressions using properties of exponents

Simplifying power and exponential expressions using properties of exponents

Simplifying an expression with both power and exponential functions using properties of exponents
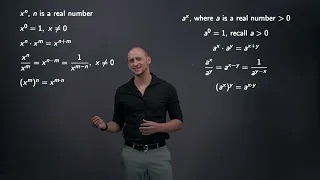
Properties of exponents applied to power and exponential expressions

Properties of multiplying and simplifying power and exponential expressions

Properties of exponents applied to power and exponential expressions

Expanding logarithmic expressions using logarithm rules

Condensing a logarithmic expression into a single logarithm

Explaining the terminology and rules of logarithms

Finding horizontal asymptotes for rational functions
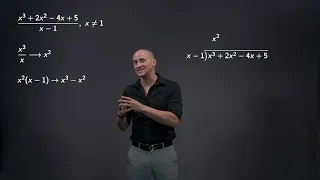
Explaining how to do polynomial long division

Finding horizontal asymptotes for rational functions

Determining the end behavior and horizontal asymptotes for rational functions

Explaining basic algebraic operations for fractions

How to simplify rational expressions

Adding and subtracting rational expressions by finding a common denominator

Explaining how to multiply and divide rational expressions
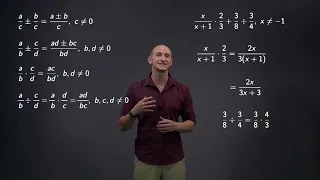
Performing algebraic operations with rational expressions and simplifying the answer

Introducing functions of several variables and level curves

Evaluating and then finding and sketching the domain of a function of two variables

Finding and sketching the domain of a function of two variables

Sketching the level curves for a function of two variables

Sketching the level curves for a function of two variables

Sketching the level curves for a function of two variables

Explaining that a graph is a collection of vertices and edges

Drawing a graph to depict a bus route

Counting the vertices and edges from a graph

Identifying the adjacent vertices in a graph

Finding two different paths between vertices in a graph

Determining if a list of vertices in a graph is a path, circuit, Euler path, Euler circuit, or none of the above

Determining if a list of vertices in a graph is a path, a circuits, an Euler path, an Euler circuit, or none of the above

Determining if a list of vertices in a graph is a path, a circuits, an Euler path, an Euler circuit, or none of the above

Determining if a list of vertices in a graph is a path, a circuits, an Euler path, an Euler circuit, or none of the above

Determining if a list of vertices in a graph is a path, a circuits, an Euler path, an Euler circuit, or none of the above

Determining if a list of vertices in a graph is a path, a circuits, an Euler path, an Euler circuit, or none of the above

Explaining Euler's Theorem on when a graph has an Euler path or Euler circuit

Finding the valence of each vertex in a graph

Explaining Hamiltonian Circuits and paths, the Method of Trees to find them, and the number of Hamiltonian circuits for complete graphs

Determining if a graph has a Hamiltonian path, Hamiltonian Circuit, or neither

Determining if a graph has a Hamiltonian path, Hamiltonian Circuit, or neither

Determining if a graph has a Hamiltonian path, Hamiltonian Circuit, or neither

Determining if a graph has a Hamiltonian path, Hamiltonian Circuit, or neither

Using the method of trees to find all Hamiltonian circuits of a graph starting at a given vertex

Determining if a graph is a complete graph

Determining if a graph is a complete graph

Determining if a graph is a complete graph

Determining if a graph is a complete graph

Finding two spanning trees for a graph

Introducing functions of several variables and level curves

Explanation of graphs for data and which are appropriate for categorical or numerical data

Finding all solutions to a trigonometric equation with sine

Solving a trigonometric equation with secant by factoring

Solving a trig equation with sine and cosine using aPythagorean Identity

Solving a system of linear equations and giving a geometric interpretation of the solution

Solving a system of two linear equations in two unknowns by graphing

Finding the coordinate vector of a quadratic given a basis for the vector space

Solving a rational equation and checking the solutions

Solving an equation with logarithmic functions

Solving an equation with logarithmic functions

Determining if a graph represents a function and finding the domain and range

Finding the properties of a quadratic function such as the vertex, axis of symmetry, intercepts, etc.

Factoring a quadratic polynomial

Factoring a quadratic function

Factoring a quadratic where the leading coefficient is 1

Factoring quadratics where the leading coefficient is not 1

Factoring a sum of cubes and a difference of cubes

Finding the composition of a rational function and a quadratic

Finding and simplifying the difference quotient for a quadratic function

Solving an inequality with a quadratic by factoring and using a sign diagram

Finding the absolute maximum or absolute minimum of a quadratic

Writing the standard form of quadratic function given its vertex and one other point