
Sine, Cosine, and Tangent
Explaining the trigonometric ratios of right triangles for sine, cosine, and tangent
Problem: Find the length of side \(a\) in the triangle below.


Explaining the trigonometric ratios of right triangles for sine, cosine, and tangent

Finding the six trigonometric ratios for a right triangle

Using trig to find an angle in a right triangle with two given sides

Explaining the special right triangles and the relationships between their sides

Finding the exact value of tangent for several given angles using the unit circle

Using the unit circle to sketch the graph of the tangent function

Graphing the reciprocal trig functions cosecant, secant, and cotangent

Using the double angle identities for cosein to derive the half-angle identities for sine and cosine

Using the Pythagorean Trig Identity to derive the secondary Pythagorean Identities

Using the Half-Angle Identities to find the exact values of sine, cosine, and tangent

Using the Reciprocal, Ratio, and Pythagorean Identities to verify a trig identity

Proving a trig identity involving sine, cosine, and cotangent

Solving a trigonometric equation with tangent and sine by factoring

Solving a trig equation with sine and tangent using a trig identity

Evaluating all six trigonometric functions for a right triangle

Evaluating all six trigonometric functions for a right triangle

Using trigonometry to determine the height of a tree

Evaluating trigonometric functions given a point on the terminal side of an angle

Evaluating trigonometric functions given a point on the terminal side of an angle

Finding trigonometric functions given information about the angle

Finding the values of all six trigonometric functions of an angle given a right triangle

Evaluating the other five trigonometric functions for an acute angle given the value of sine

Evaluating the other five trigonometric functions given sine and that tangent is negative

Evaluating compositions with inverse trigonometric functions

Writing an equivalent algebraic expression for compositions with inverse trigonometric functions containing variables

Using inverse trigonometry to write an expression for an angle in a right triangle

Verifying a trigonometric identity

Solving a trigonometric equation

Solving a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Using a difference formula to evaluate a trigonometric function

Using a sum formula to evaluate a trigonometric expression

Using a sum formula to evaluate a trigonometric expression

Finding the properties of a transformed tangent function and graphing it

Review of limits and derivatives of inverse trigonometric functions
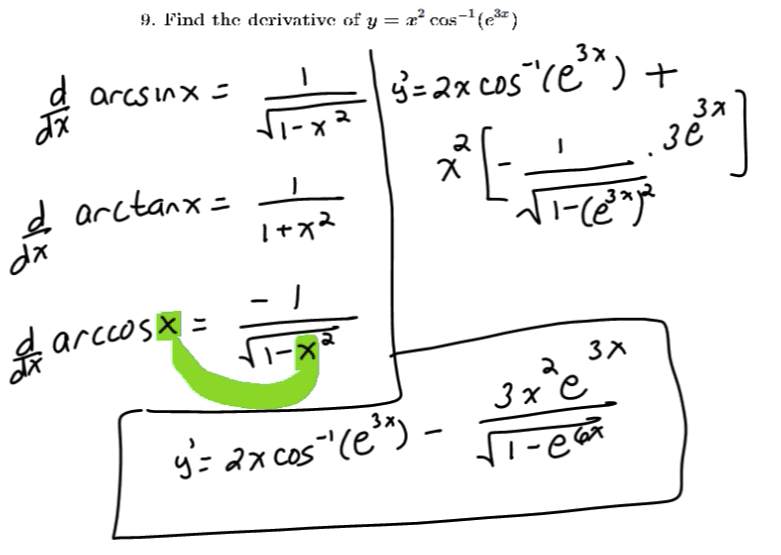
Review of limits and derivatives of inverse trigonometric functions

Properties and derivatives of inverse trigonometric functions

Properties and derivatives of inverse trigonometric functions

Simplifying expressions containing trigonometric and inverse trigonometric functions

Evaluating compositions of trigonometric and inverse trigonometric functions

Calculating a composition of tangent and arcsine

Review of trigonometric substitution

Using trigonometric identities to integrate powers of secant and tangent

Review of limits and derivatives of inverse trigonometric functions

Review of limits and derivatives of inverse trigonometric functions

Properties of inverse trig functions and the derivative of arctangent

Properties and derivatives of inverse trigonometric functions

Proving the derivatives of trigonometric functions and that sine is continuous

Properties of inverse trig functions and the derivative of arctangent

Properties and derivatives of inverse trigonometric functions

Review of trigonometric substitution

Using trigonometric identities to integrate powers of secant and tangent

Integrating using a trigonometric substitution

Explaining the Pythagorean Theorem and using it to find a missing side in a right triangle

Special Right Triangles Exercise 1

Special Right Triangles Exercise 2

Finding the values of trig functions with the unit circle

Finding the exact value of secant, cosecant, and cotangent using the unit circle

Finding the exact values of cosine and cotangent for given angles using the unit circle

Finding the exact values of sine and secant for several given angles using the unit circle

Finding the angles where sine has a given value using the unit circle

Finding the angle where secant has a given value and tangent is positive

Using the unit circle to sketch the graph of the sine function

Using the unit circle to sketch the graph of the cosine function

Graphing a period of a transformed sine function

Graphing a period of a transformed cosine function

Writing the sine and cosine functions for a given graph

Using the reciprocal and ratio trig identities to simplify an expression

Using the Pythagorean Identities to simplify a trig expression

Using the sum identities of sine and cosine to derive the double angle identities

Using the difference identities of sine and cosine to derive the cofunction identities

Using the Sum and Difference Identities to find the exact value of cosine

Using the Sum Identity for Trig to find the exact value of sine

Using a Double Angle Identity to find the exact value of an expression with sine and cosine

Proving a trigonometric identity involving secant, cotangent, and tangent

Proving a trig identity involving sine and cosine

Finding all solutions to a trigonometric equation with sine

Solving a trigonometric equation with sine and cosine by factoring

Solving a trigonometric equation with secant by factoring

Solving a trig equation with sine and cosine using trig identities

Solving a trig equation with cosine using trig identities

Solving a trig equation with cotangent and sine using trig identities

Using the Even/Odd and Cofunction Identities to solve an equation with sine

Solving a trig equation with sine and cosine using aPythagorean Identity

Solving a trig equation with cotangent and cosecant using trig identities

Using trigonometry to determine the edge lengths of a right triangle

Evaluating all six trigonometric functions for angles in degrees and radians

Evaluating a composition of tangent and arccosine

Finding the solutions to an equation with tangent in a given interval

Solving a limit example with a trigonometric functions

Solving a limit example with a trigonometric function

Evaluating a trigonometric limit using trigonometric identities

Determining the properties of a sine function and graphing it

Writing the equation for a sine function with certain characteristics

Determining the properties of a cosine function and graphing it

Writing the equation for a cossine function with certain characteristics

Writing the equation for a sine function to match a given graph

Writing the equation for a cosine function to match a given graph

Evaluating compositions with inverse trigonometric functions

Evaluating a composition of trigonometric and inverse trigonometric functions

Verifying a trigonometric identity

Solving a trigonometric equation

Solving a trigonometric equation by factoring

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Using double angle formulas to evaluate trigonometric functions

Using a sum formula to rewrite a trigonometric expression

Using the Law of Sines to solve a triangle

Using the Law of Sines to solve a triangle

Using the Law of Cosines to solve a triangle

Using the Law of Sines to solve a triangle

Derivatives and vectors with some physics applications

Review of the limit definition of a derivative and calculating the derivative

Derivatives of exponential functions and the exponential model

Reviewing the chain rule and the derivatives and limits of trigonometric functions

Review of the limit definition of a derivative and calculating the derivative

Review of derivatives and tangent lines to functions and vector equations
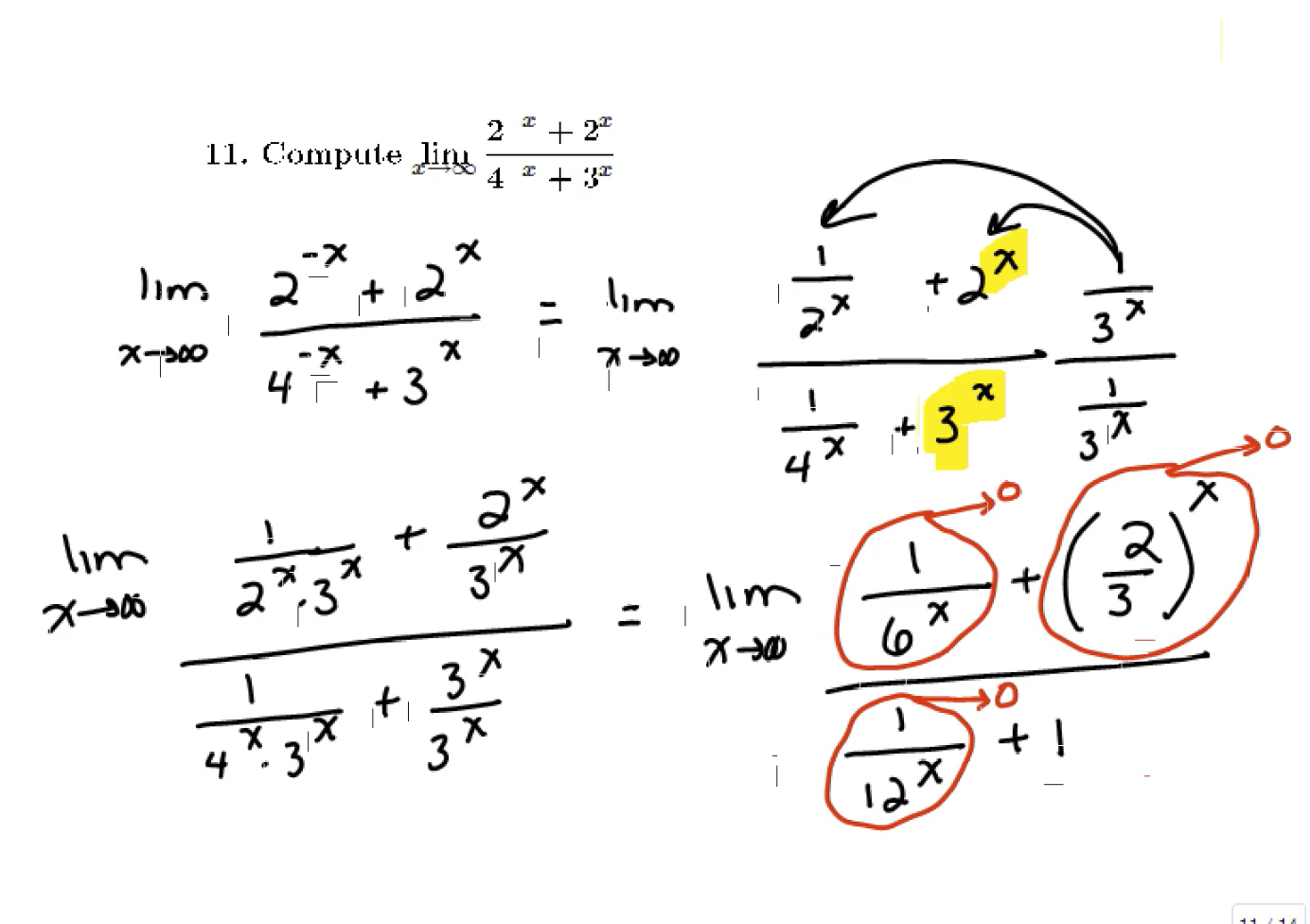
Approximation and Newton's Method, and limits and derivatives of exponential functions

Limits at infinity and asymptotes, along with physics applications

Limits at infinity, asymptotes, and tangent lines

Review of the limit definition of a derivative and calculating the derivative

Review of derivatives and tangent lines to functions and vector equations

Differentials, linear approximations and quadratic approximations

Review of the limit definition of a derivative and calculating the derivative

Derivatives and tangents to curves

Derivatives of trigonometric functions and using the Chain Rule
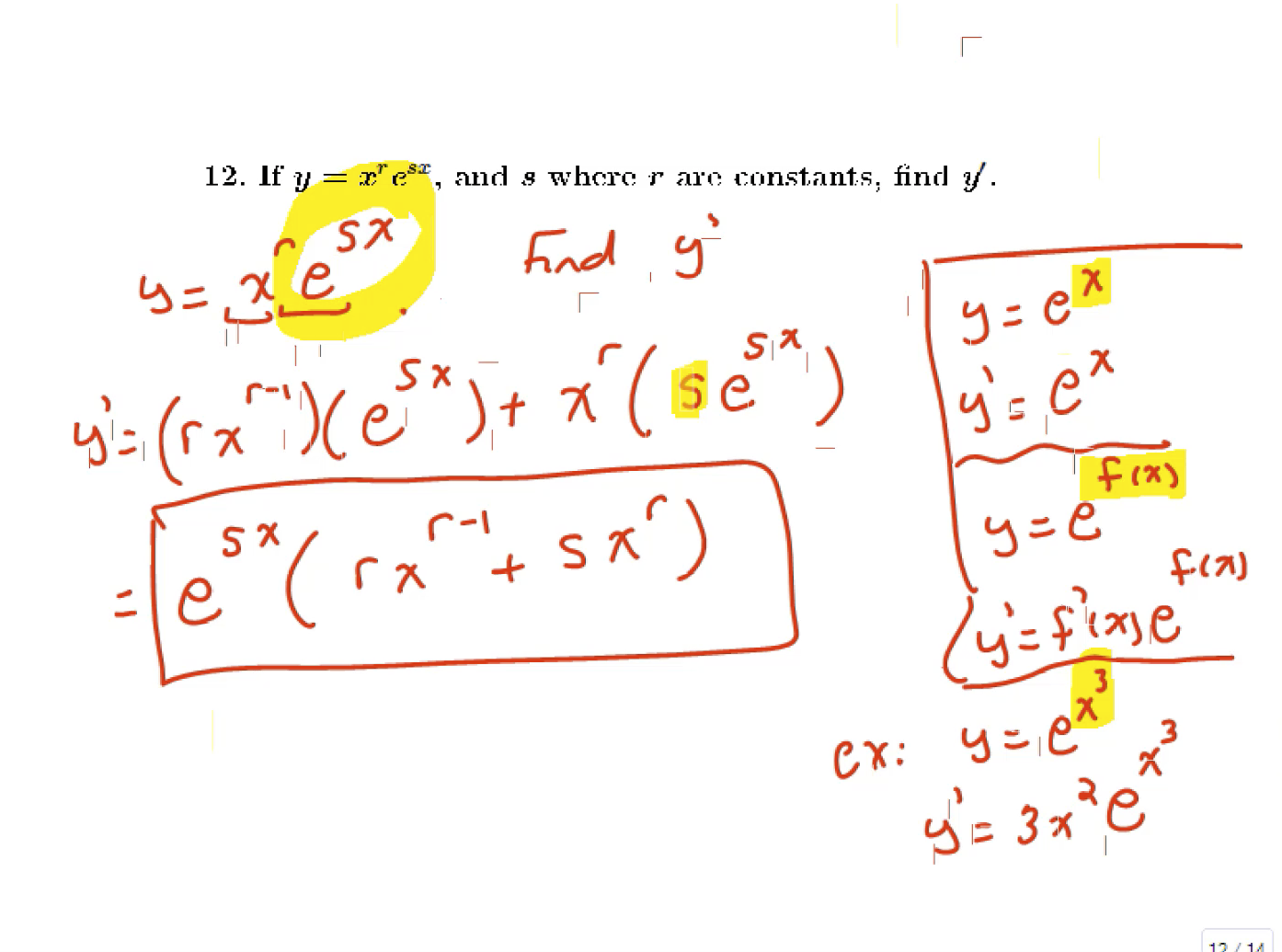
Approximation and Newton's Method, and limits and derivatives of exponential functions

Derivatives of trigonometric functions and using the Chain Rule

Derivatives and vectors with some physics applications
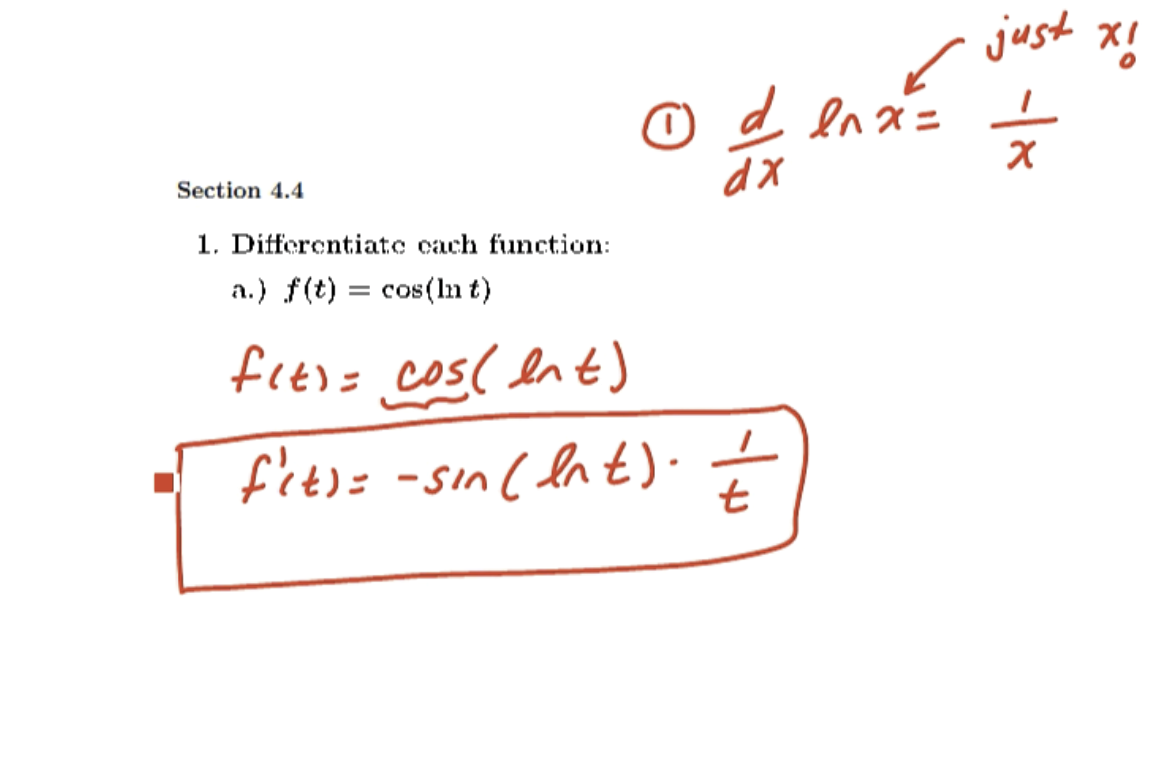
Derivatives of exponential and logarithmic functions and the exponential model

Derivatives and vectors with some physics applications

Derivatives of exponential and logarithmic functions and the exponential model

Using derivatives to find properties of graphs
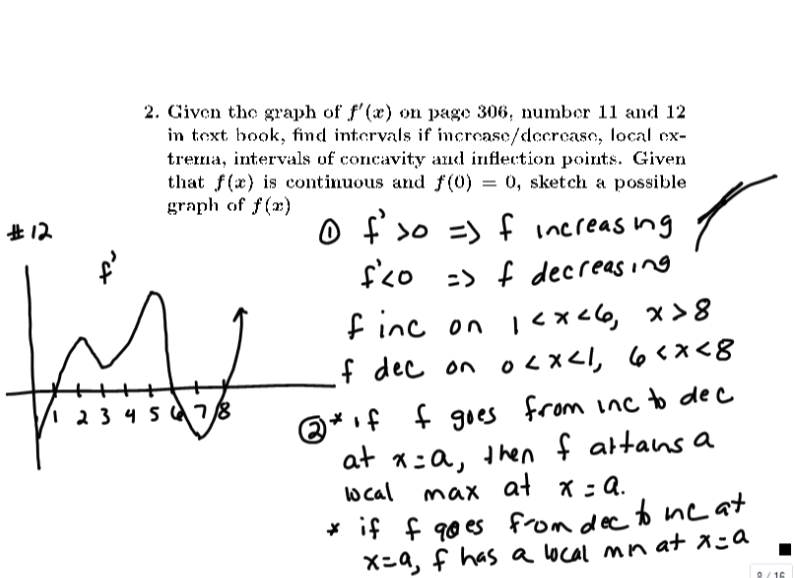
Using derivatives to find properties of graphs

Using L'Hospital's Rule to solve limits

Evaluating a composition of trigonometric and inverse trigonometric functions

Finding a Cartesian equation for a parametric curve

Using vectors to find the magnitude and direction of a resultant force

Using the Chain Rule to differentiate functions with exponential and trigonometric functions

Using the Chain Rule to differentiate a function containing trigonometric functions

Using the Product, Quotient and Chain Rules to find several derivatives

Using the Quotient and Chain Rules to find several derivatives

Finding the derivative of an implicit function

Finding the derivative of an implicit function

Finding the antiderivative of a function with secant and tangent

Converting parametric equations into a Cartesian equation

Determining the rate that the area of a triangle is increasing based on the rate an angle is increasing

Converting parametric equations into a Cartesian equation and graphing

Converting parametric equations into a Cartesian equation and graphing

Evaluating an integral using integration by parts

Evaluating an integral using trigonometric identities

Evaluating an integral using trigonometric identities

Using trigonometric identities to integrate powers of sine and cosine

Using a trigonometric identity to integrate powers of secant and tangent

Using a trigonometric identity to integrate powers of secant and tangent

Using trigonometric identities to integrate powers of cosine and tangent

Integrating a function with sine using u-substitution

Explaining the cases for using trigonometric substitution

Using trigonometric substitution to evaluate an indefinite integral

Using trigonometric substitution to evaluate an indefinite integral

Using trigonometric substitution to evaluate an indefinite integral

Using trigonometric substitution to evaluate an indefinite integral

Using trigonometric substitution to evaluate a definite integral

Using trigonometric substitution to evaluate a definite integral
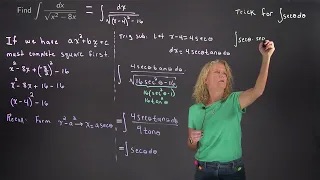
Using trigonometric substitution to evaluate an indefinite integral
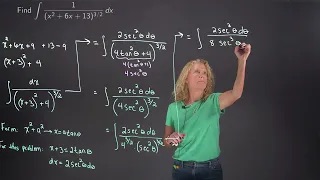
Using trigonometric substitution to evaluate an indefinite integral

Proving facts about the derivatives of vector functions including the product rule

Derivatives and vectors with some physics applications

Review of the limit definition of a derivative and calculating the derivative

Derivatives of exponential functions and the exponential model

Reviewing the chain rule and the derivatives and limits of trigonometric functions

Review of the limit definition of a derivative and calculating the derivative

Review of derivatives and tangent lines to functions and vector equations

Proving a property of scalar multiplication for limits using the epsilon-delta definition and using the Squeeze Theorem for Limits.

Approximation and Newton's Method, and limits and derivatives of exponential functions

Limits at infinity and asymptotes, along with physics applications

Limits at infinity, asymptotes, and tangent lines

Review of the limit definition of a derivative and calculating the derivative

Review of derivatives and tangent lines to functions and vector equations

Differentials, linear approximations, and quadratic approximations

Review of the limit definition of a derivative and calculating the derivative

Review of derivatives and tangent lines to functions and vector equations

Derivatives of trigonometric functions and using the Chain Rule
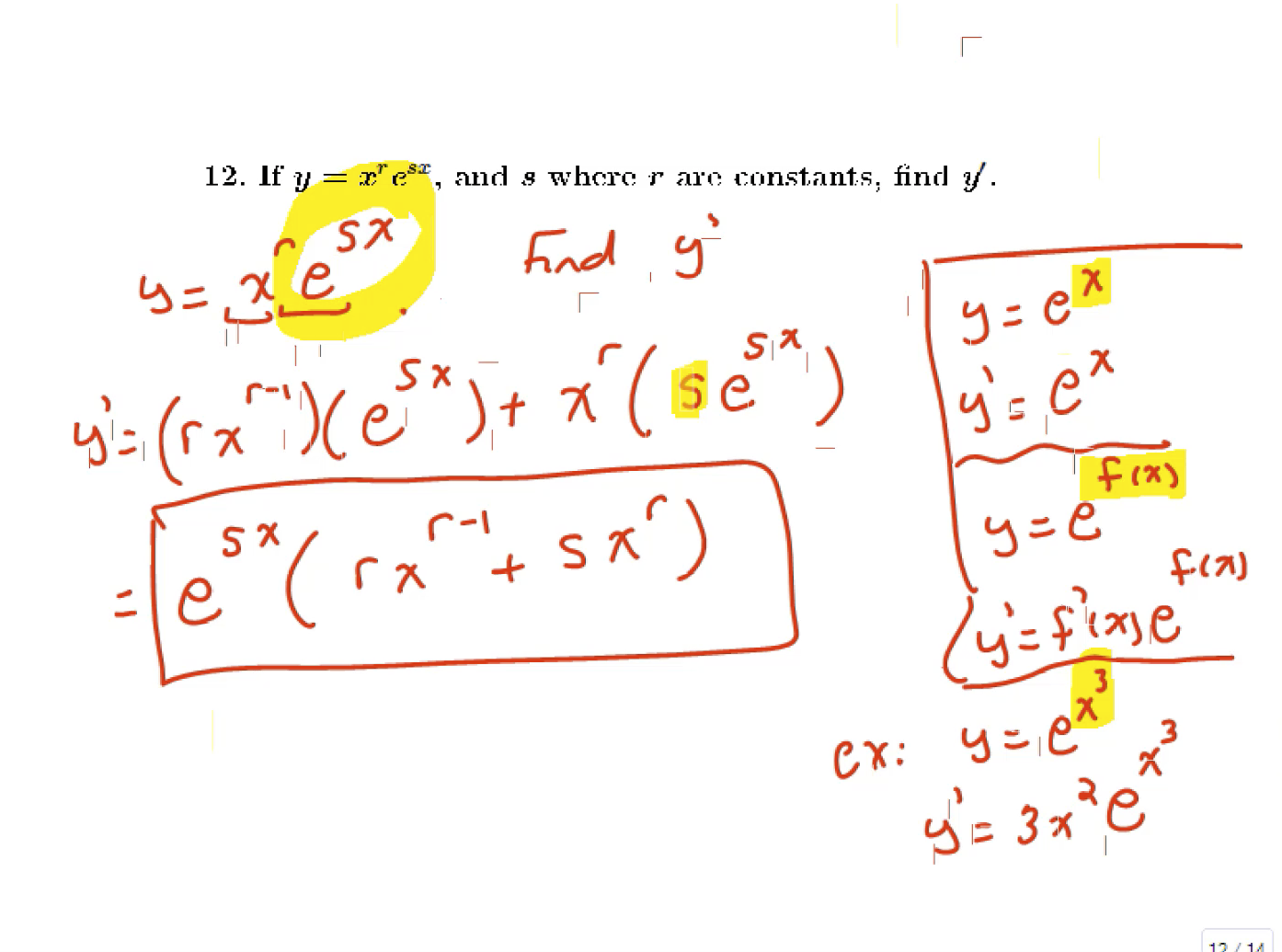
Approximation and Newton's Method, and limits and derivatives of exponential functions

Derivatives of trigonometric functions and using the Chain Rule

Derivatives and vectors with some physics applications
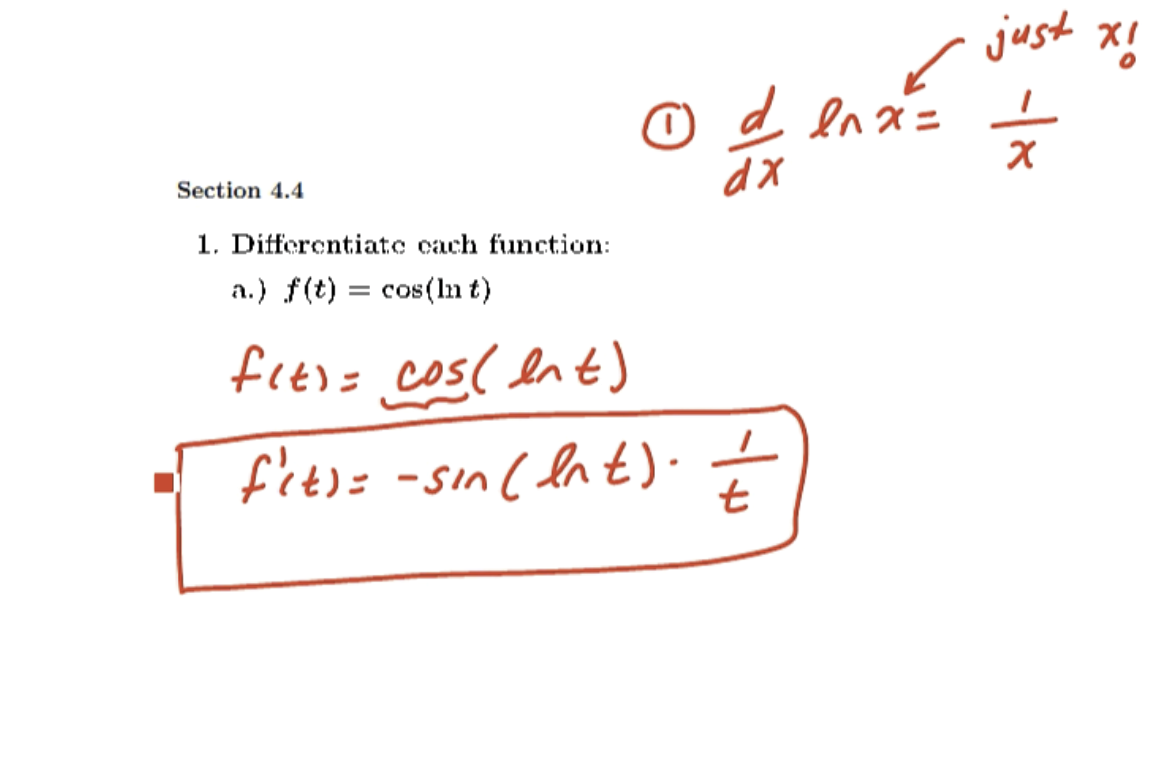
Derivatives of exponential and logarithmic functions and the exponential model

Using derivatives to find properties of graphs

Using derivatives to find properties of graphs

Using L'Hospital's Rule to solve limits

Using u substitution to evaluate integrals and prove facts about logarithms and integrals and

Proving the Fundamental Theorem of Calculus and examples of u Substitution

Interpreting integrals to represent areas between curves

Proving trigonometric identities useful for integration

Using trigonometric identities to integrate powers of sine and cosine

Explaining the cases for using trigonometric substitution

Finding a partial fraction decomposition and integrating using partial fractions

Evaluating a double integral over a rectangle

Determining if a sequence is increasing, decreasing, or not monotonic and if it is bounded

Using a rotation map matrix to rotate a 2-dimensional vector by the angle \(\pi\)

Discussing the degree and radian measure of special angles on the unit circle

The coordinates for the quadrantal angles on the unit circle

Finding the coordinates on the unit circle for the common angles in the first quadrant

Finding the coordinates on the unit circle for all the common angles

Defining radians for angle measure using the corresponding arc length on a unit circle

Converting an angle measured in degrees to radians

Converting angles measured in radians to degrees

How to find reference angles for angles in standard position

Defining coterminal angles and how to determine if angles are coterminal

Drawing an angle in standard position

Finding a negative and positive coterminal angle for a given angle

Drawing an angle in standard position and finding its reference angle

Drawing an angle in standard position and finding its reference angle

Finding a coterminal angle along with its reference angle and graphing it

Finding a coterminal angle along with its reference angle and graphing it

Finding the values of \(\theta\) that makes a matrix with trig functions invertible

Determining whether trigonometric functions are linearly independent

Finding the dimension of the subspace spanned by a set of functions

Solving a trigonometric equation with sine and cosine on a given interval

Solving an quadratic-like equation with sine by factoring

Solving an equation with cosine on a given interval

Solving a trigonometric equation with sine on a given interval

Sketching one period of a transformed sine graph

Finding the amplitude, period, phase shift, and vertical shift for a given sine function

Writing a cosine function for a given graph

Solving equations symbolically in Python and interpreting the results