
Sine, Cosine, and Tangent
Explaining the trigonometric ratios of right triangles for sine, cosine, and tangent
Problem: Use Even/Odd Identities and Cofunction identities to find all x in \([0, 2\pi]\) satisfying \(-\frac{1}{2}=\sin\left( -\frac{\pi}{2}+x \right).\)
Solution: \(x=\dfrac{\pi}{3}, \dfrac{5\pi}{3}\)
Solution Method: This is a case where we’ll use multiple trig identities to solve a trigonometric equation. In this case, cofunction and even/odd identities. Cofunction identities are a special case of the sum/difference identites. Even/Odd identities derive from cosine being an even function and sine and tangent being odd functions. You can easily verify that these functions and even and odd respectively by looking at their graphs. Cosine has y-axis symmetry, so it’s even. Sine and tangent have origin symmetry, and are odd.
Comparing my expression to the identities, I notice that \(\sin\left( -\frac{\pi}{2}+x \right)\) is very close to the cofunction identity \(\cos{x}= \sin\left( \frac{\pi}{2}-x \right)\). I just need to distribute out a negative to make them match. \[\begin{aligned} -\frac{1}{2}&=\sin\left( -\frac{\pi}{2}+x \right) \\ -\frac{1}{2}&=\sin\left( -(\frac{\pi}{2}-x) \right) \end{aligned}\] Then by the odd identity of sine, that negative can come out of the argument. \[\begin{aligned} -\frac{1}{2}&=-\sin\left( \frac{\pi}{2}-x\right) \end{aligned}\] So now I can apply the cofunction identity, \[\begin{aligned} -\frac{1}{2} &= -\cos{x} \\ \frac{1}{2} &= \cos{x} \end{aligned}\] So now we’re looking for values of x in the interval \([0,2\pi]\) that satisfy this. That interval is just the unit circle so I need to remember what special angles produce cosine of one-half on the unit circle. First, this is a positive half so I can only have angle values in Q1 and Q4. Cosine corresponds to the x-values on the unit circle and I know that my x-coordinate is one-half for reference angle values of \(\frac{\pi}{3}\). In Q1, that is just \(\frac{\pi}{3}\), in Q4 it is \(\frac{5\pi}{3}\). So the values of x in \([0, 2\pi]\) satisfying the equation are \(\frac{\pi}{3}\) and \(\frac{5\pi}{3}\).

Explaining the trigonometric ratios of right triangles for sine, cosine, and tangent

Finding the six trigonometric ratios for a right triangle

Using the reciprocal and ratio trig identities to simplify an expression

Using the Pythagorean Identities to simplify a trig expression

Using the Pythagorean Trig Identity to derive the secondary Pythagorean Identities

Using the sum identities of sine and cosine to derive the double angle identities

Using the difference identities of sine and cosine to derive the cofunction identities

Using the Sum and Difference Identities to find the exact value of cosine

Using the Sum Identity for Trig to find the exact value of sine

Using a Double Angle Identity to find the exact value of an expression with sine and cosine

Using the Half-Angle Identities to find the exact values of sine, cosine, and tangent

Using the Reciprocal, Ratio, and Pythagorean Identities to verify a trig identity

Proving a trigonometric identity involving secant, cotangent, and tangent

Proving a trig identity involving sine and cosine

Proving a trig identity involving sine, cosine, and cotangent

Solving a trig equation with sine and cosine using aPythagorean Identity

Solving a trig equation with cotangent and cosecant using trig identities

Solving a trig equation with sine and tangent using a trig identity

Solving a trig equation with sine and cosine using trig identities

Solving a trig equation with cosine using trig identities

Solving a trig equation with cotangent and sine using trig identities

Evaluating a trigonometric limit using trigonometric identities

Verifying a trigonometric identity

Verifying a trigonometric identity

Using a double angle formula to solve a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Using a double angle formula to solve a trigonometric equation

Solving a trigonometric equation by factoring

Using double angle formulas to evaluate trigonometric functions

Using a difference formula to evaluate a trigonometric function

Using a sum formula to evaluate a trigonometric expression

Using a sum formula to evaluate a trigonometric expression

Using a sum formula to rewrite a trigonometric expression

Evaluating a composition of trigonometric and inverse trigonometric functions

Finding a Cartesian equation for a parametric curve

Converting parametric equations into a Cartesian equation

Converting parametric equations into a Cartesian equation and graphing

Converting parametric equations into a Cartesian equation and graphing

Using trigonometric identities to integrate powers of sine and cosine

Using trigonometric identities to integrate powers of secant and tangent

Proving trigonometric identities useful for integration

Using trigonometric identities to integrate powers of sine and cosine

Using trigonometric identities to integrate powers of secant and tangent

Using trig to find the length of the side of a right triangle given an angle and side length

Using trig to find an angle in a right triangle with two given sides

Explaining the special right triangles and the relationships between their sides

Finding the values of trig functions with the unit circle

Finding the exact value of tangent for several given angles using the unit circle

Finding the exact value of secant, cosecant, and cotangent using the unit circle

Finding the exact values of cosine and cotangent for given angles using the unit circle

Finding the exact values of sine and secant for several given angles using the unit circle

Finding the angles where sine has a given value using the unit circle

Finding the angle where secant has a given value and tangent is positive

Using the unit circle to sketch the graph of the sine function

Using the unit circle to sketch the graph of the cosine function

Using the unit circle to sketch the graph of the tangent function

Graphing the reciprocal trig functions cosecant, secant, and cotangent

Graphing a period of a transformed sine function

Graphing a period of a transformed cosine function

Writing the sine and cosine functions for a given graph

Using the double angle identities for cosein to derive the half-angle identities for sine and cosine

Finding all solutions to a trigonometric equation with sine

Solving a trigonometric equation with sine and cosine by factoring

Solving a trigonometric equation with secant by factoring

Solving a trigonometric equation with tangent and sine by factoring

Finding the values of \(\theta\) that makes a matrix with trig functions invertible

Solving a limit example with a trigonometric functions

Solving a limit example with a trigonometric function

Determining the properties of a sine function and graphing it

Writing the equation for a sine function with certain characteristics

Determining the properties of a cosine function and graphing it

Writing the equation for a cossine function with certain characteristics

Writing the equation for a sine function to match a given graph

Writing the equation for a cosine function to match a given graph

Evaluating compositions with inverse trigonometric functions

Evaluating compositions with inverse trigonometric functions

Writing an equivalent algebraic expression for compositions with inverse trigonometric functions containing variables

Using inverse trigonometry to write an expression for an angle in a right triangle

Evaluating a composition of trigonometric and inverse trigonometric functions

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Solving a trigonometric equation

Using the Law of Sines to solve a triangle

Using the Law of Sines to solve a triangle

Using the Law of Cosines to solve a triangle

Using the Law of Sines to solve a triangle

Finding the properties of a transformed tangent function and graphing it

Review of limits and derivatives of inverse trigonometric functions
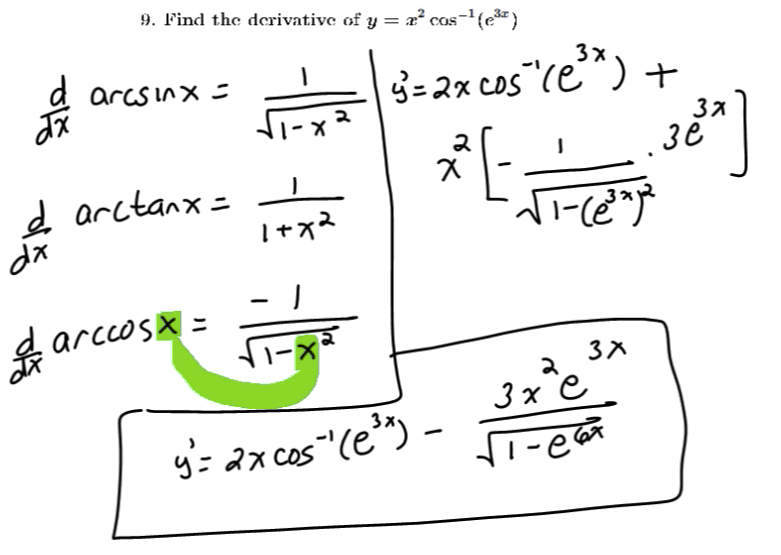
Review of limits and derivatives of inverse trigonometric functions

Properties and derivatives of inverse trigonometric functions

Properties and derivatives of inverse trigonometric functions

Simplifying expressions containing trigonometric and inverse trigonometric functions

Using vectors to find the magnitude and direction of a resultant force

Evaluating compositions of trigonometric and inverse trigonometric functions

Calculating a composition of tangent and arcsine

Review of trigonometric substitution

Finding the Maclaurin series of a function

Evaluating an integral using trigonometric identities

Evaluating an integral using trigonometric identities

Evaluating an integral using trigonometric identities

Evaluating an integral using trigonometric identities

Evaluating an integral using trigonometric identities

Using trigonometric identities to solve an integral with powers of sine and cosine

Using trigonometric identities to integrate a power of cosine

Using a trigonometric identity to integrate powers of sine and cosine

Using a trigonometric identity to integrate powers of sine and cosine

Using trigonometric identities to integrate even powers of sine and cosine

Using a trigonometric identity to integrate an even power of cosine

Using a trigonometric identity to integrate powers of secant and tangent

Using a trigonometric identity to integrate powers of secant and tangent

Using trigonometric identities to integrate powers of cosine and tangent

Integrating a function with sine using u-substitution

Explaining the cases for using trigonometric substitution

Using trigonometric substitution to evaluate an indefinite integral

Using trigonometric substitution to evaluate an indefinite integral

Using trigonometric substitution to evaluate an indefinite integral

Using trigonometric substitution to evaluate an indefinite integral

Using trigonometric substitution to evaluate a definite integral

Using trigonometric substitution to evaluate a definite integral
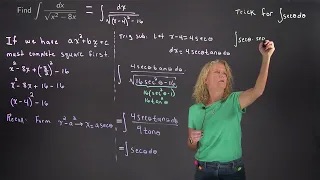
Using trigonometric substitution to evaluate an indefinite integral
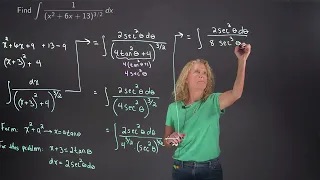
Using trigonometric substitution to evaluate an indefinite integral

Proving facts about the derivatives of vector functions including the product rule

Review of limits and derivatives of inverse trigonometric functions

Review of limits and derivatives of inverse trigonometric functions

Properties of inverse trig functions and the derivative of arctangent

Properties and derivatives of inverse trigonometric functions

Proving a property of scalar multiplication for limits using the epsilon-delta definition and using the Squeeze Theorem for Limits.

Proving the derivatives of trigonometric functions and that sine is continuous

Properties and derivatives of inverse trigonometric functions

Properties of inverse trig functions and the derivative of arctangent

Using u substitution to evaluate integrals and prove facts about logarithms and integrals and

Review of trigonometric substitution

Interpreting integrals to represent areas between curves

Integrating using a trigonometric substitution

Explaining the cases for using trigonometric substitution

Finding a partial fraction decomposition and integrating using partial fractions

Using a rotation map matrix to rotate a 2-dimensional vector by the angle \(\pi\)

Explaining the Pythagorean Theorem and using it to find a missing side in a right triangle

Special Right Triangles Exercise 1

Special Right Triangles Exercise 2

Discussing the degree and radian measure of special angles on the unit circle

The coordinates for the quadrantal angles on the unit circle

Finding the coordinates on the unit circle for the common angles in the first quadrant

Finding the coordinates on the unit circle for all the common angles

Defining radians for angle measure using the corresponding arc length on a unit circle

Converting an angle measured in degrees to radians

Converting angles measured in radians to degrees

How to find reference angles for angles in standard position

Defining coterminal angles and how to determine if angles are coterminal

Drawing an angle in standard position

Finding a negative and positive coterminal angle for a given angle

Drawing an angle in standard position and finding its reference angle

Drawing an angle in standard position and finding its reference angle

Finding a coterminal angle along with its reference angle and graphing it

Finding a coterminal angle along with its reference angle and graphing it

Determining whether trigonometric functions are linearly independent

Finding the dimension of the subspace spanned by a set of functions

Using trigonometry to determine the edge lengths of a right triangle

Evaluating trigonometric functions given a point on the terminal side of an angle

Evaluating trigonometric functions given a point on the terminal side of an angle

Finding trigonometric functions given information about the angle

Evaluating all six trigonometric functions for angles in degrees and radians

Evaluating all six trigonometric functions for a right triangle

Evaluating all six trigonometric functions for a right triangle

Using trigonometry to determine the height of a tree

Finding the values of all six trigonometric functions of an angle given a right triangle

Evaluating the other five trigonometric functions for an acute angle given the value of sine

Evaluating the other five trigonometric functions given sine and that tangent is negative

Evaluating a composition of tangent and arccosine

Finding the solutions to an equation with tangent in a given interval

Solving a trigonometric equation with sine and cosine on a given interval

Solving an quadratic-like equation with sine by factoring

Solving an equation with cosine on a given interval

Solving a trigonometric equation with sine on a given interval

Sketching one period of a transformed sine graph

Finding the amplitude, period, phase shift, and vertical shift for a given sine function

Writing a cosine function for a given graph